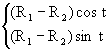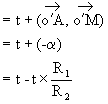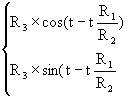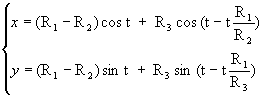Il s'agit de simuler sur ordinateur le jeu du Spirograph. Ce jeu est un jeu à dessiner composé de pignons dentés en plastique qui roulent les uns sur les autres et qui permettent d'obtenir de jolies figures, comme par exemple :

Sur cet exemple, on dispose un pignon fixe à 133 dents et on fait rouler, à l'intérieur de celui-ci, un second pignon à 58 dents. Le stylo qui permet de tracer la courbe est inséré dans le trou n° 25 du pignon mobile.

Mathématiquement, la courbe obtenue est une sorte d'hypocycloïde dont les équations, bien que pas très compliquées, relèvent au moins du niveau spécialité mathématique en terminale S. Nous nous contenterons donc d'admettre les équations paramétriques données plus loin.

Dans le jeu réel, on ne peut choisir que parmi 2 pignons fixes :

• un pignon comportant 96 dents à l'intérieur et 144 dents à l'extérieur,
• un pignon comportant 105 dents à l'intérieur et 150 dents à l'extérieur.

De même, le choix du pignon mobile est limité à 13 possibilités (24, 30, 32, 45, 48, 52, 56, 60, 63, 72, 80 et 84 dents). Ces pignons possèdent un certains nombre de trous (une dizaine pour les pignons les plus petits à une trentaine pour les plus grands) dans lesquels on insère un stylo de couleur quelconque.

Dans l'exemple ci-contre, on fait rouler le pignon mobile à 72 dents à l'intérieur du pignon fixe à 105 dents.

Si on met le stylo dans le trou n° 20, on obtient le dessin reproduit en dessous.

Le principal avantage de l'ordinateur, par rapport au jeu réel, réside dans la facilité de réaliser les dessins sans faire déraper le stylo ... De plus, un peut faire varier le nombre de dents comme on veut, ainsi que le nombre de trous.

On peut essayer de comprendre comment fonctionne le spirograph en observant le dessin suivant :

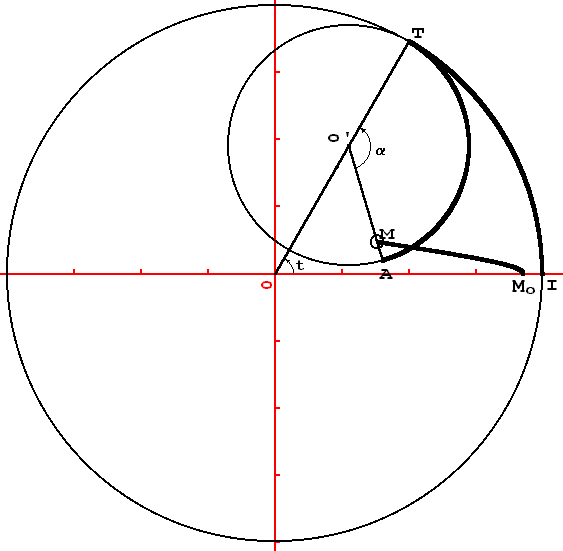
Le cercle fixe, C₁, a pour centre o et pour rayon R₁ = oI = 4.

Le cercle mobile, C₂, tangent intérieurement à C₁ au point T, a pour centre o' et pour rayon R₂ = o'T = 1,8.

Le trou dans lequel se trouve le crayon, se trouve dans le cercle C₂ au point M tel que :
o'M = R₃ = 1,5.

Si le cercle C₂ roule sans glisser et sans patiner dans C₁, alors l'arc IT a la même longueur que l'arc AT.

Lorsque le cercle C₂ roule dans C₁ à partir du point de contact I jusqu'au point de contact T, le point-crayon dessine la ligne M₀M.

Notons t une mesure en radians de l'angle 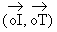. La longueur de l'arc IT est donc R₁´t.
Notons a une mesure en radians de l'angle 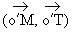. La longueur de l'arc AT est donc R₂´a.
On en déduit : R₂´a= R₁ ´t. Donc : .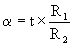
D'après la relation de Chasles : .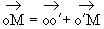
Or oo' = R₁-R₂.
Donc 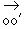a pour coordonnées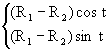
De plus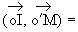
                            
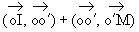
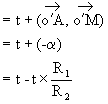
Donc 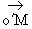a pour coordonnées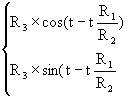
On en déduit les coordonnées de 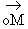, donc du point M :

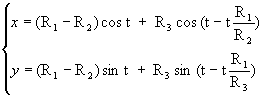
Dans l'exemple ci-dessus, le paramètre t varie de 0 à 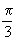, mais si on fait varier t dans l'intervalle [-9p, 9p], on obtient la figure complète :

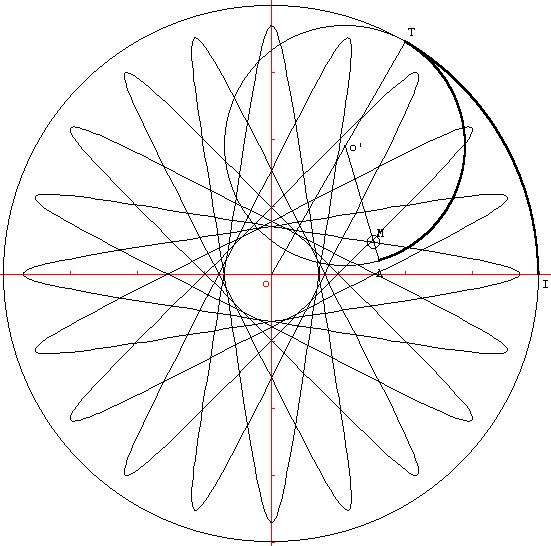
Il faut en effet, faire 9 tours complets à l'intérieur de C₁ pour que la courbe dessinée se referme. Le nombre de tours nécessaires se calcule à partir des rayons R₁ et R₂. On calcule d'abord le PPMC de R₁ et de R₂ (c'est-à-dire le plus petit multiple commun). On trouve 36 lorsque R₁ = 4 et R₂ = 1,8. Ensuite, il suffit de diviser 36 par R₁ et le tour est joué.

Bien entendu, les 3 paramètres R₁, R₂ et R₃ permettent de faire varier à l'infini le dessin obtenu. Dans la pratique, on doit avoir R₁>R₂>R₃, mais rien n'empêche de continuer à utiliser les mêmes équations même si cette condition n'est pas vérifiée : les dessins obtenus sont dans ce cas impossible à obtenir avec le jeu réel.

La fiche principale, que l'on peut nommer fmSpirograph, possède les propriétés suivantes :

• name = fmSpirograph
• caption = Spirograph
• color = clWhite

En bas de la fiche principale, on pourra mettre un composant " Panel " dont les principales propriétés sont :

• Align = alBottom
• Caption = vide

Ce " panel " (dont on peut laisser le nom par défaut Panel1) servira à mettre les composants qui serviront de contrôles pour l'utilisateur :

Quatre composants " Label " dont les propriétés caption sont respectivement :

• Couleur :
• Pignon fixe :
• Pignon mobile :
• Trou n° :

Trois boutons dont les noms sont :

• BtEffacer
• BtDessiner
• BtQuitter
  

On pourra par la suite ajouter un bouton pour imprimer ...

Trois composants " Edit " dont les noms sont :

• EdFixe (pour saisir le nombre de dents du pignons fixe)
• EdMobile (idem pour le pignon mobile)
• EdTrou (pour saisir le n° du trou)

Trois composants " UpDown " qui contrôlent les contenus des 3 composants précédents :

• UdFixe (valeurs extrêmes 20 à 200, position = 133)
• UdMobile (valeurs extrêmes 20 à 200, position = 58)
• UdTrou (valeurs extrêmes 0 à 100, position = 25)

On n'oubliera pas d'associer les 3 composants " UpDown " aux 3 composants " Edit ".

Un composant " ColorGrid " que l'on peut nommer cgCouleur.
4. La fonction qui calcule le PPMC de 2 entiers.

Nous l'avons vu, cette fonction est nécessaire pour déterminer le nombre de tours requis pour obtenir la figure complète.

Voici cette fonction :

function PPMC(a,b:integer):integer;
//calcule le plus petit multiple commun à a et b
var x,y,r : integer;
begin
x:=a;
y:=b;
repeat //recherche du PGDC de x et y par l'algorithme d'Euclide
r:=a mod b;
if r>0 then
begin
a:=b;
b:=r;
end;
until r=0;
PPMC:=(x*y)div b; //b est le PGDC de x et y
end;

C'est la procédure qui permet de lancer le dessin en réponse à un clic sur le bouton dessiner :

procedure TfmSpirograph.btDessinerClick(Sender: TObject);
var k,R1,R2,R3 : integer;
    t,dt,x0,y0,x,y : real;
begin
   if btDessiner.caption='Arrêter' then
   begin
      btDessiner.Caption:='Dessiner';
   end
   else btDessiner.caption:='Arrêter';
   R1:=2*udFixe.Position;
   R2:=2*udMobile.Position;
   R3:=2*udTrou.Position;
   k:=PPMC(R1,R2)div R1;
   t:=0;
   dt:=0.1;
   x0:=width/2;
   y0:=(clientheight-panel1.height)/2;
   x:=x0+(R2-R1)*cos(t)+R3*cos(t-t*R1/R2);
   y:=y0+(R2-R1)*sin(t)+R3*sin(t-t*R1/R2);
   with canvas do
   begin
      MoveTo(round(x),round(y));
      pen.Color:=cgCouleur.ForegroundColor;
      repeat
         if btDessiner.caption='Dessiner' then exit;
         t:=t+dt;
         x:=x0+(R2-R1)*cos(t)+R3*cos(t-t*R1/R2);
         y:=y0+(R2-R1)*sin(t)+R3*sin(t-t*R1/R2);
         LineTo(round(x),round(y));
         sleep(10);
         application.ProcessMessages;
      until t>k*2*pi;
   end;
   btDessiner.Caption:='Dessiner';
end;

procedure TfmSpirograph.btEffacerClick(Sender: TObject);
begin
   with canvas do
   begin
      brush.color:=clWhite;
      brush.style:=bsSolid;
      rectangle(0,0,width,height);
      brush.Style:=bsClear;
   end;
end;

Il ne reste plus qu'à écrire la procédure associée au bouton " Quitter " et à faire des essais de dessins.