Il s’agit de réaliser un programme permettant de rechercher tous les triplets pythagoriciens possibles compris entre 2 valeurs données.

Un triplet pythagoricien est formé de 3 nombres entiers naturels a, b et c tels que a² + b² = c², autrement dit, 3 entiers naturels qui peuvent être les longueurs de 3 côtés d’un triangle rectangle.

Par exemple, il y a 6 triplets pythagoriciens compris entre 1 et 20. Ce sont (3, 4, 5), (5, 12, 13), (6, 8, 10), (8, 15, 17), (9, 12, 15) et (12, 16, 20).

Le programme doit permettre à l’utilisateur de définir les bornes (1 et 20 dans l’exemple ci-dessus) puis de lancer la recherche.

Effectuer la commande Fichier / Nouvelle application
Renommer la fiche « Form1 » en « fmTripletsPythagoriciens » (propriété name)
Mettre le titre « Triplets pythagoriciens » dans la propriété caption de la fiche principale
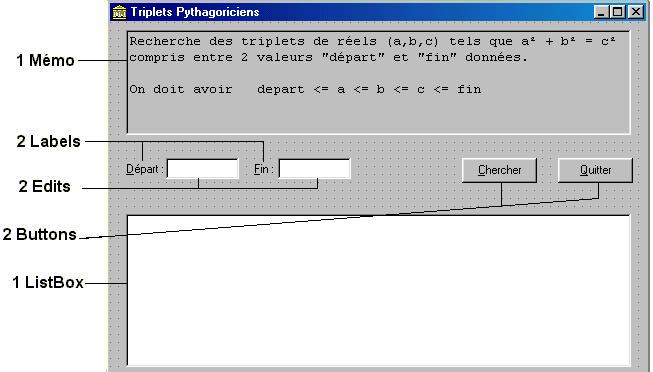
Placer dans la fiche principale, les composants suivants, selon la disposition indiquée :

3. Enregistrer tout

Dans votre dossier, créez un dossier nommé « Triplets pythagoriciens »
Dans le dossier que vous venez de créer, enregistrez Unit1 sous « uTripletsPythagoriciens »
Dans ce même dossier, enregistrez Project1 sous « TripletsPythagoriciens »

4. Initialisation de la fiche principale

• Il s’agit de définir les variables globales qui vont être utilisées et de contrôler leur état au moment du lancement du programme.
• Ajouter les variables globales dont nous aurons besoin :

var
   fmTripletsPythagoriciens: TfmTripletsPythagoriciens;
   depart,fin : integer;

implementation

• Sélectionner la fiche principale et, dans l’inspecteur d’objets, onglets événements, faire un double clic dans la zone de saisie OnActivate, puis compléter le texte de la procédure ainsi :

procedure TfmTripletsPythagoriciens.FormActivate(Sender: TObject);
begin
   Depart:=0;
   Fin:=0;
end;

5. Réponse à un clic de souris sur le bouton Quitter

Procéder comme pour le TP précédent sur le nombre mystérieux.
Lancer l’exécution pour vérifier que le bouton Quitter fonctionne bien.
Enregistrer tout.

6. Contrôle de la validité des saisies de l’utilisateur

Normalement, les composants edDepart et edFin ne doivent accepter que des entiers naturels. De plus, la valeur du composant edFin doit être supérieure strictement à celle du composant edDepart.

Ces fonctions sont assurées de la façon suivante :

• Sélectionner le composant edDepart et, dans l’inspecteur d’objets, onglet Evénements, faire un double clic dans la zone de saisie de l’événement OnChange, puis compléter la procédure :

procedure TfmTripletsPythagoriciens.edDepartChange(Sender: TObject);
var erreur : integer;
begin
   val(edDepart.text,depart,erreur);
   btChercher.enabled:=(erreur=0)and(depart<fin);
end;

• Faire la même chose avec le composant edFin, mais cette fois, le texte est le suivant :

procedure TfmTripletsPythagoriciens.edFinChange(Sender: TObject);
var erreur : integer;
begin
   val(edFin.text,Fin,erreur);
   btChercher.enabled:=(erreur=0)and(depart<fin);
end;

Explications : la procédure val permet de transformer une donnée de type chaîne de caractères en un nombre entier. La syntaxe de cette procédure est Val(ch,nombre,erreur) où ch est une chaîne de caractères, nombre est la variable qui reçoit la valeur numérique et erreur est une variable qui est égale à 0 s’il ne se produit aucune erreur pendant la conversion. Si erreur est non nul, cela signifie que la chaîne ch n’était pas un nombre entier. La chaîne à traduire se trouve dans la propriété text du composant edDepart ou du composant edFin. Pour l’atteindre on écrit edDepart.text ou edFin.text.
La propriété enabled du bouton btChercher prend la valeur true (le bouton chercher devient actif) lorsque la variable erreur est nulle et lorsque depart<fin. Si l’une de ces 2 conditions n’est pas remplie alors la propriété enabled prend la valeur false et le bouton chercher devient inactif (il ne pourra pas réagir à un clic de souris)

• Enregistrer tout
• Lancer l’exécution pour vérifier que tout fonctionne bien (sauf le bouton chercher qui, pour l’instant, ne peut pas réagir car nous n’avons pas dit ce qu’il devait faire… :) )

7. Réponse à un clic de souris sur le bouton Chercher

Il s’agit évidemment de la procédure clé.

• Sélectionner le bouton btChercher


• Dans l’inspecteur d’objets, onglet Evénements, faire un double-clic dans la zone de saisie de l’événement OnClic et compléter la procédure :

procedure TfmTripletsPythagoriciens.btChercherClick(Sender: TObject);
var a,b,c : integer;
    ch : string;
begin
   lbListeTriplets.Clear;
   screen.Cursor:=crHourGlass; //curseur sablier pendant les calculs
   for a:=depart to fin-2 do
      for b:=a to fin-1 do
         for c:=b to fin do
            if a*a+b*b=c*c then
            begin
               ch:=inttostr(a)+', '+inttostr(b)+', '+inttostr(c);
               lbListeTriplets.Items.Add(ch);
               lbListeTriplets.Refresh;
            end;
   screen.Cursor:=crDefault; //on rétablit le curseur normal
end;

Explications

On fait varier les variables a, b et c entre les valeurs depart et fin à l’aide de structures « for ». Cette structure est très semblable à celle que l’on peut trouver sur les calculatrices Casio ou Texas. Nous en étudierons le détail plus tard. Dans cet exemple , il y a 3 structures FOR imbriquées les unes dans les autres ce qui a pour effet de faire « tourner » les valeurs de a, b et c à la manière des chiffres dans un compteur kilométrique de voiture : a correspond au chiffre des centaines de km, b correspond au chiffre des dizaines et c correspond au chiffre des unités. La seule différence est que, dans le cas du compteur kilométrique, les chiffres varient de 0 à 9 tandis qu’ici, le nombre a varie dans l’intervalle [depart, fin–2], le nombre b varie dans l’intervalle [a, fin–1] et le nombre c varie dans l’intervalle [b, fin].
Lorsqu’un triplet (a, b, c) répond au critère de Pythagore, on l’ajoute au composant ListBox nommé lbListeTriplets. Un tel composant permet d’afficher, en colonnes bien alignées, des chaînes de caractères. Ce composant est vidé au début, grâce à l’instruction : lbListeTriplets.clear. Ensuite on utilise sa méthode Add pour lui ajouter, au fur et à mesure du déroulement, les chaînes composées des 3 nombres séparés par une virgule et un espace. La méthode Refresh du composant lbListeTriplets permet de mettre à jour l’affichage à chaque fois qu’une nouvelle chaîne est ajoutée.

• Lancer l’exécution du programme pour tester son bon fonctionnement.


• Essayer d’agrandir la fenêtre en cliquant sur le bouton . L’effet est décevant n’est-ce pas ?

8. Modification de la taille des composants lorsqu’on redimensionne la fenêtre

Tous les composants visuels possèdent une propriété très intéressante qui permet de les redimensionner lorsqu’on modifie la taille d’une fenêtre. Il s’agit de la propriété Anchors (ancres en français).

• Sélectionner le composant MemoInformation


• Dans l’inspecteur d’objets, onglets Propriétés, cliquer sur le signe + qui se trouve à gauche de la propriété Anchors : ceci permet de visualiser les 4 ancrages possibles du composant. Par défaut, les composants sont ancrés sur le bord gauche et sur le bord supérieur de la fenêtre. Nous pouvons modifier ce comportement en mettant à True les variables akLeft, akTop et akRight, et en mettant à False la variable akBottom. Ainsi, lorsqu’on agrandira la fenêtre, les bords gauche, haut et droit du composant MemoInformation suivront les bords gauche, haut et droit de la fenêtre.


• Procéder de la même façon pour ancrer à gauche et en haut, les 2 Labels et les 2 Edits (il n’y a sans doute rien à modifier car ce sont les ancrages par défaut).


• Faire de même pour ancrer en haut et à droite, les 2 boutons Chercher et Quitter.


• Faire enfin de même pour ancrer dans les 4 directions, le composant lbListeTriplets.


• Lancer l’exécution de l’application et agrandir puis réduire la fenêtre principale pour contrôler le bon comportement des différents composants sur la fiche.

9. Affichage du nombre de triplets obtenus

• Ajouter, par exemple juste au-dessus du composant lbListeTriplets, un composant Label avec les propriétés suivantes :
  - name : lblNombreDeTriplets
  - font : choisir une police un peu plus grande que la police par défaut, en gras.
• Modifier le code de la procédure btChercherClick de la façon suivante (les modifications sont en gras) :

procedure TfmTripletsPythagoriciens.btChercherClick(Sender: TObject);
var a,b,c : integer;
    ch : string;
begin
   lbListeTriplets.Clear;
   screen.Cursor:=crHourGlass; //curseur sablier pendant les calculs
   for a:=depart to fin-2 do
      for b:=a to fin-1 do
         for c:=b to fin do
            if a*a+b*b=c*c then
            begin
               ch:=inttostr(a)+', '+inttostr(b)+', '+inttostr(c);
               lbListeTriplets.Items.Add(ch);
               lblNombreDeTriplets.Caption:=IntToStr(lbListeTriplets.Items.
                   Count)+' triplet(s) trouvé(s)';
               lbListeTriplets.Refresh;
               lblNombreDeTriplets.Refresh;
            end;
   screen.Cursor:=crDefault; //on rétablit le curseur normal
end;

• Enregistrer tout
• Relancer l’application pour essayer les modifications.

10. Amélioration de la vitesse de calcul

Lorsque les valeurs depart et fin deviennent grandes, les calculs sont nettement plus longs. Il est possible de réduire cette durée en supprimant l’une des boucles FOR dans la procédure btChercherClick. Voici les modifications :

procedure TfmTripletsPythagoriciens.btChercherClick(Sender: TObject);
var a,b,c : integer;
    ch : string;
begin
   lbListeTriplets.Clear;
   screen.Cursor:=crHourGlass;
   for a:=depart to fin-2 do
      for b:=a to fin-1 do
      begin
         c:=round(sqrt(a*a+b*b));
         if (a*a+b*b=c*c)and(c<=fin) then
         begin
            ch:=inttostr(a)+', '+inttostr(b)+', '+inttostr(c);
            lbListeTriplets.Items.Add(ch);
            lblNombreDeTriplets.Caption:=IntToStr(lbListeTriplets.Items.
                  Count)+' triplet(s) trouvé(s)';
            lbListeTriplets.Refresh;
            lblNombreDeTriplets.Refresh;
         end;
      end;
   screen.Cursor:=crDefault;
end;

Explications :

Plutôt que de faire varier c dans un intervalle en essayant toutes les valeurs possibles, on calcule la valeur arrondie à l’entier le plus proche de . La fonction racine carrée se nomme sqrt en langage Pascal et la fonction qui permet d’arrondir le résultat à l’entier le plus proche est round. Voyons cela sur 2 exemples :
- Si on prend a = 5 et b = 7 alors ce qui donne 9 après avoir arrondi. Comme , le triplet (5, 7, 9) n’est pas ajouté à la liste.
- Si, par contre, a = 5 et b = 12 alors , ce qui est arrondi à …13 naturellement. Comme 5² + 12² = 13², le triplet (5, 12, 13) est ajouté à la liste.

11. Prolongements possibles

On peut rechercher les quadruplets (a, b, c, d) tels que : a² + b² + c² = d² par exemple.

<< TP précédent        TP suivant >>

Retour à la liste des TP