2.1. Principe de la planche de Galton
Galton (1822-1911) était le cousin de Darwin et voulait justifier
la transmission des capacités intellectuelles par l'hérédité
pour permettre l'amélioration de l'espèce humaine. Son point
de départ était le paradoxe suivant : comment expliquer qu'on
observe à chaque génération une dispersion des tailles,
qu'à celle des parents devra s'ajouter celle des enfants et, qu'en
même temps la taille des individus d'une population et la dispersion
par rapport à chaque moyenne reste constante quand les générations
se succèdent ? .
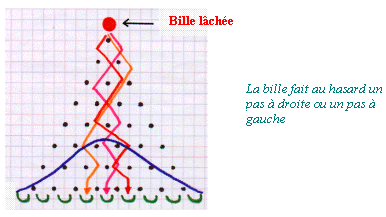
Pour comprendre le phénomène, Galton réalisa une expérience
à l'aide d'un plan incliné sur lequel il planta des clous
disposés en quinconce. En faisant tomber un grand nombre de billes,
en haut du plan incliné, on observe une répartition à
l'arrivée qui suit une loi binomiale. Cette loi peut être approchée
(théorème de la limite centrale) par la loi normale ou loi
de Gauss.
Voici 2 adresses internet (parmi d'autres) qui donnent des complément d'information. La première de ces adresses contient en particulier une simulation de l'expérience écrite en java :
http://www-sop.inria.fr/mefisto/java/tutorial1/node11.html
http://www.seti-quebec.org/chronique/simon/sem4/rouge.htm
On peut également voir cette expérience à la Cité des sciences de la Vilette à Paris. Le stand montrant la planche de Galton est celui qui attire le plus de visiteurs :
2.2. Simulation de la planche de Galton sur Excel
La planche
de Galton sera la feuille de calcul. Les clous seront remplacés par
des cellules noires disposées en quinconce comme ci-contre.
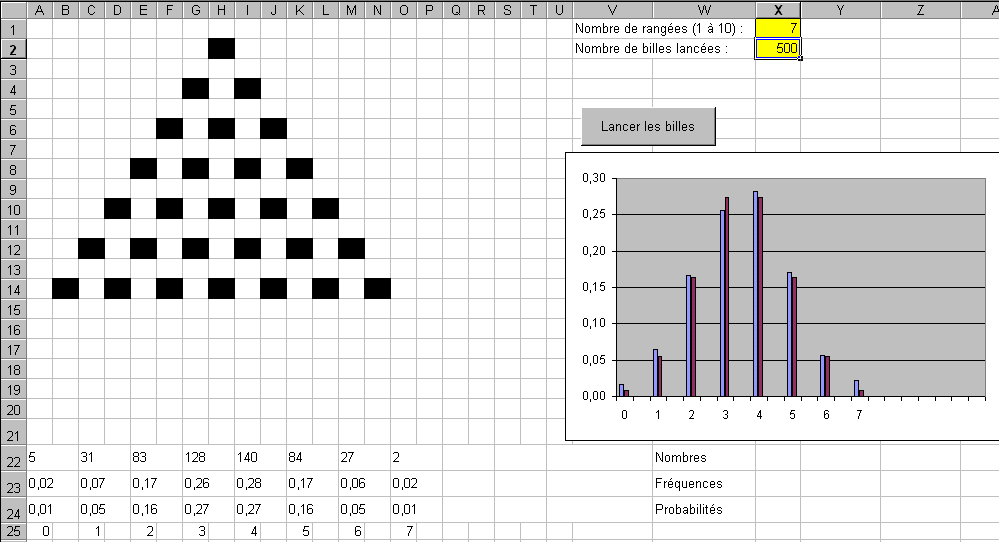
Le nombre de rangées de cellules noires sera choisi par l'utilisateur, ainsi que le nombre de billes à lancer.
Un histogramme permettra de montrer les fréquences obtenues pour chacune des colonnes réceptrices ainsi que les probabilités théoriques.
Voici comment peut se précenter la feuille de calcul une fois terminée :
2.3. Initialisation
Il faut d'abord régler manuellement les largeurs et hauteurs des cellules comme ci-dessus et regrouper par 2 les cellules des lignes 22, 23 et 24.
De même, il faut remplir manuellement les cellules V1 et V2 ainsi que les cellules X1 et X2.
La procédure Initialisation va permettre de mettre en place les " clous " (cellules noires) et d'effacer les données des lancers précédents.
Voici l'algorithme qui permet de faire cette initialisation :
Début Initialisation Effacer la plage de cellules A1 à U21 NombreRangées <— Cellule X1 'NombreRangées doit être une variable globale NombreBilles <— cellule X2 'NombreBilles doit être aussi une var. globale Pour L <— 1 à NombreRangées Pour C <— NombreRangées+2-L à NombreRangées+1+L par pas de 2 Colorier l'intérieur de la cellule(2L, C) en noir FinPour FinPour Effacer le contenu (pas le format) de la plage de cellules A22 à V25 Initialiser le générateurs de nombres aléatoires Fin Initialisation
2.4. Procédure Lancer
Il s'agit de la procédure principale qui est associée au bouton " lancer les billes ". Les billes seront lâchées une à une et seront visualisées par une brève coloration en rouge de chacune des cellules traversées.
L'algorithme de cette procédure est le suivant :
Début LancerLesBilles Initialisation Pour bille <— 1 à NombreBilles C <— NombreRangées+1 'correspond à la colonne du milieu de la planche Pour L <— 1 à NombreRangées Mettre brièvement la cellule (2L-1,C) en rouge X <— Nombre aléatoire compris entre 0 et 1 Si X<0.5 alors C <— C-1 'déplacement de la bille vers la gauche Sinon C <— C+1 'déplacement de la bille vers la droite FinSi Mettre brièvement la cellule (2L-1,C) en rouge Mettre brièvement la cellule (2L,C) en rouge Mettre brièvement la cellule (2L+1,C) en rouge FinPour Cellule(22,C) <— cellule(22,C)+1 'nombre de billes tombées dans C Cellule(23,C) <— Cellule(23,C)/bille 'fréquence des billes tombées en C FinPour Pour C <— 0 à NombreRangées Cellule(24,2C+1)( probabilité que la boule tombre dans la colonne C Si Cellule(23,2C+1) est vide alors Cellule(23,2C+1) <— 0 Cellule(25,2C+1) <— C FinPour Fin LancerLesBilles
Cette procédure fait appel plusieurs fois à la même
action appliquée sur des cellulles différentes Mettre
brièvement la cellule (L,C) en rouge. Voici comment on peut
réaliser cette procédure :
Sub Allume(Ligne, Colonne)
Cells(Ligne, Colonne).Interior.ColorIndex = 3
'j = 0 pour ralentir la trajectoire de la bille
'Do While j < 100000
' j = j + 1
'Loop
Cells(Ligne, Colonne).Interior.ColorIndex = 0
End Sub
Enfin, la probabilité que la boule tombe dans la colonne C suit la loi binomiale B(NombreRangées, 0.5). On peut l'obtenir facilement :
Function Prob(C)
r = 1
n = C
Do While n > 0
r = r * (NombreRangées + 1 - n) / n
n = n - 1
Loop
r = r * 0.5 ^ C * 0.5 ^ (NombreRangées - C)
Prob = r
End Function
2.5. Graphique
Il suffit de sélectionner la zone de données A23 à V25 et de bien construire le graphique en fonction des indications fournies par l'assistant graphique.