1.1. Polygones réguliers
Deux méthodes sont possibles :
-
On peut dessiner successivement les n côtés du polygone. Dans ce cas, la figure dessinée ne peut pas être déplacée d'un seul coup avec la souris : il faut déplacer les segments un à un. Autre inconvénient : il n'est pas possible de colorier l'intérieur du polygone. Par contre, c'est la méthode la plus simple.
-
On peut construire le polygone en utilisant la méthode BuildFreeForm. Dans ce cas, le polygone est considéré comme un seul objet et peut être déplacé à la souris. L'intérieur peut être colorié ...
Voici ces 2 méthodes :
'Dessiner un polygone régulier
'TP 8 ICES année 2002
Const pi = 3.141592656
Sub DessinerPolygone()
ActiveSheet.Lines.Delete
x = Cells(1, 2) 'abscisse du centre du polygone
y = Cells(2, 2) 'ordonnée du centre du polygone
r = Cells(3, 2) 'rayon du cercle circonscrit au polygone
n = Cells(4, 2) 'nombre de côtés du polygone
x1 = x + r '(x1, y1) = point de départ du dessin
y1 = y
For k = 1 To n
x2 = x + r * Cos(2 * k * pi / n)
y2 = y + r * Sin(2 * k * pi / n)
ActiveSheet.Lines.Add x1, y1, x2, y2
x1 = x2
y1 = y2
Next
End Sub
Sub DessinerPolygoneBis()
x = Cells(1, 2) 'abscisse du centre du polygone
y = Cells(2, 2) 'ordonnée du centre du polygone
r = Cells(3, 2) 'rayon du cercle circonscrit au polygone
n = Cells(4, 2) 'nombre de côtés du polygone
With ActiveSheet.Shapes.BuildFreeform(msoEditingCorner, x + r, y)
For k = 1 To n
x2 = x + r * Cos(2 * k * pi / n)
y2 = y + r * Sin(2 * k * pi / n)
.AddNodes msoSegmentLine, msoEditingAuto, x2, y2
Next
Set Polygone = .ConvertToShape
End With
Polygone.Line.ForeColor.SchemeColor = 4
Polygone.Fill.Transparency = 0
Polygone.Fill.ForeColor.SchemeColor = 5
Polygone.Fill.OneColorGradient msoGradientHorizontal, 1, 1
End Sub
1.2. Triangle de Pascal
Pas de difficulté particulière. La solution avait été donnée en cours :
'Triangle de Pascal (15 premières lignes)
'Exercice du TP 8 - ICES année 2002
Sub Pascal()
Cells(1, 1) = 1
For L = 2 To 15
For C = 1 To L
If C = 1 Then
Cells(L, C) = 1
Else
Cells(L, C) = Cells(L - 1, C - 1) + Cells(L - 1, C)
End If
Next C
Next L
End Sub
1.3. Nombres parfaits
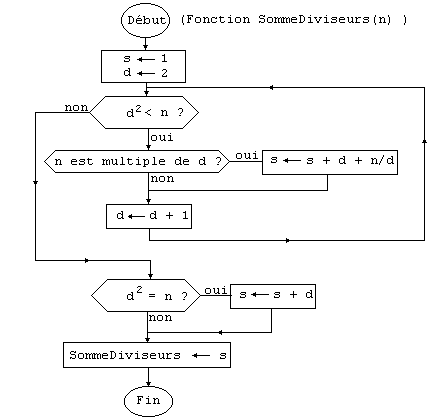
Certains n'ont peut-être pas pu faire cet exercice car l'organigramme n'était pas donné. Voici donc d'abord l'organigramme d'une fonction qui retourne la somme des diviseurs d'un entier n donné :
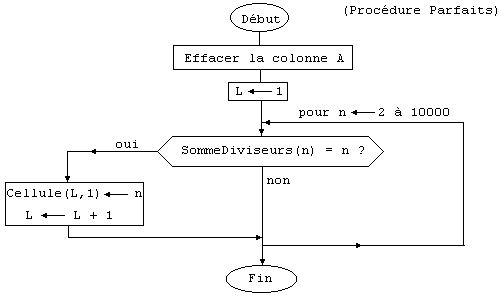
Voici maintenant l'organigramme de la procédure permettant d'afficher tous les nombres parfaits compris entre 1 et 10000 :
1.4. Anneaux olympiques
Il faut commencer par définir une procédure permettant de dessiner un anneau dont on connaît les coordonnées du centre (x , y), le rayon intérieur (r1), le rayon extérieur (r2)et la couleur (couleur). Plusieurs techniques permettent d'obtenir ce résultat, mais la méthode la plus simple est la suivante :

On pourra se reporter au TP3 pour savoir comment utiliser la méthode
AddShape
Le programme principal est alors très simple (attention, les codes des couleurs ne sont peut être pas les mêmes sur I-Mac) :
Sub AnneauOlympique()
ActiveSheet.DrawingObjects.Delete
Anneau 100, 100, 38, 47, 4 'anneau de couleur bleue
Anneau 200, 100, 38, 47, 5 'anneau de couleur jaune
Anneau 300, 100, 38, 47, 0 'anneau de couleur noire
Anneau 150, 150, 38, 47, 3 'anneau de couleur verte
Anneau 250, 150, 38, 47, 2 'anneau de couleur rouge
End Sub
1.5. Tableau " pointes et fils "
L'organigramme était donné et le programme qui en découle est très simple :
Sub PointesEtFils()
ActiveWindow.DisplayGridlines = False
x1 = 50
y1 = 50
x2 = 300
y2 = 250
dx = (x2 - x1) / 50
dy = (y2 - y1) / 50
For k = 0 To 50
ActiveSheet.Shapes.AddLine x1, y1 + k * dy, x1 + k * dx, y2
ActiveSheet.Shapes.AddLine x1 + k * dx, y2, x2, y2 - k * dy
ActiveSheet.Shapes.AddLine x2, y2 - k * dy, x2 - k * dx, y1
ActiveSheet.Shapes.AddLine x2 - k * dx, y1, x1, y1 + k * dy
Next
End Sub