1.1. Jeu de la Vie

'Jeu de la vie
'ICES TP7 Mars 2002

Const MaxL = 20
Const MaxC = 20
Const NbBacteries = 100

Sub Infecter()  'Initialisation (ou ensemencement) de la population bactérienne
    Cells.Clear
    Randomize
    For i = 1 To NbBacteries
        L = 2 + Int(MaxL * Rnd)
        C = 2 + Int(MaxC * Rnd)
        Cells(L, C).Interior.ColorIndex = 3
    Next i
End Sub

Function NbCellulesInfectées(L, C)  'calcul du nombre de voisines infectées
    n = Cells(L - 1, C - 1) + Cells(L - 1, C) + Cells(L - 1, C + 1) _
        + Cells(L, C - 1) + Cells(L, C + 1) _
        + Cells(L + 1, C - 1) + Cells(L + 1, C) + Cells(L + 1, C + 1)
    NbCellulesInfectées = n
End Function

Sub GénérationSuivante()    'calcul et affichage de la génération suivante
    '1ère partie : on met 1 si la cellule est infectée, 0 sinon
    For L = 2 To 1 + MaxL
        For C = 2 To 1 + MaxC
            If Cells(L, C).Interior.ColorIndex = 3 Then Cells(L, C) = 1 Else Cells(L, C) = 0
        Next C
    Next L
    
    '2ème partie : on met à jour la population, en fonction du nombre de voisines
    '              de chaque cellule
    For L = 2 To 1 + MaxL
        For C = 2 To 1 + MaxC
            n = NbCellulesInfectées(L, C)
            If Cells(L, C) = 1 Then
                If (n < 2) Or (n > 3) Then Cells(L, C).Interior.ColorIndex = 0
            Else
                If n = 3 Then Cells(L, C).Interior.ColorIndex = 3
            End If
        Next C
    Next L
End Sub

Sub CentGénérations() 'Cette procédure peut être appelée pour éviter d'avoir
                        'à cliquer 100 fois sur le bouton...
    For n = 1 To 100
        GénérationSuivante
    Next n
End Sub

1.2. Suite de Syracuse

'Exercice Suite de Syracuse
'TP 7 ICES - Mars 2002

Sub Syracuse(c)
    'Affiche la suite de Syracuse de la colonne c
    L = 1
    u = Cells(L, c)
    Do While u > 1
        If u Mod 2 = 0 Then
            u = u / 2
        Else
            u = 3 * u + 1
        End If
        L = L + 1
        Cells(L, c) = u
    Loop
End Sub

Sub Calculs()
    Range("A2:Z500").Clear
    For c = 1 To 10
        If Cells(1, c) > 0 Then Syracuse (c)
    Next c
End Sub

Function LongueurSyracuse(n)
'calcule le nombre de termes de la suite de Syracuse dont le premier terme est n
'avant que la suite ne devienne périodique
    k = 1
    u = n
    Do While u > 1
        If u Mod 2 = 0 Then
            u = u \ 2
        Else
            u = 3 * u + 1
        End If
        k = k + 1
    Loop
    LongueurSyracuse = k
End Function

Sub PlusLongueSuiteDeSyracuse()
'Détermine la plus longue suite de Syracuse parmi toutes les suites de Syracuse
'commençant par u, avec u compris entre a et b
    a = InputBox(" a = ", "Départ de l'intervalle de recherche")
    b = InputBox(" b = ", "Fin de l'intervalle de recherche")
    PlusLongue = LongueurSyracuse(a)
    DepartPlusLongue = a
    For n = a To b
        If LongueurSyracuse(n) > PlusLongue Then
            PlusLongue = LongueurSyracuse(n)
            DepartPlusLongue = n
        End If
    Next
    Cells.Clear
    Cells(1, 1) = DepartPlusLongue
    Syracuse (1)
    MsgBox ("La plus longue suite de Syracuse commence par " & DepartPlusLongue _
           & ". Elle comporte " & PlusLongue & " termes.")
End Sub

2.1. Polygones réguliers

Il s'agit de réaliser une procédure capable de dessiner un polygone régulier dont on connaît :

• Les coordonnées (x, y) du centre ,
• Le rayon r du cercle circonscrit,
• Le nombre de côtés n.

Les données seront disposées dans les colonnes A et B et on placera un bouton permettant d'obtenir le dessin comme ci-dessous :

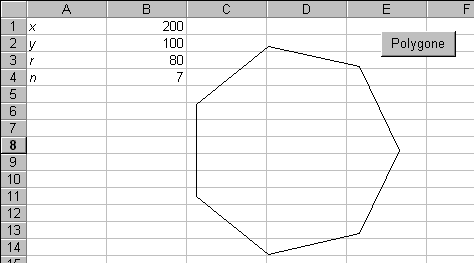
On rappelle que les coordonnées du sommet n° k d'un polygone régulier à n sommets, de centre ?(x, y) et de rayon r sont données par les formules suivantes :

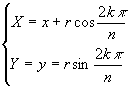
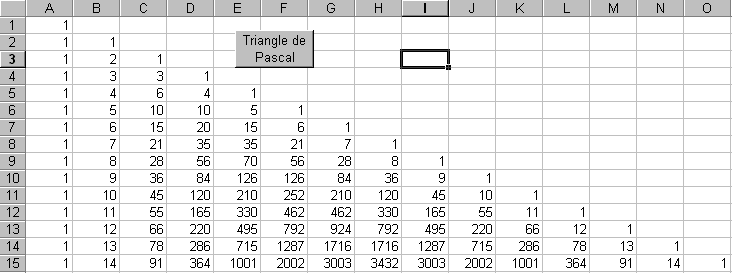
2.2. Triangle de Pascal

Définir une procédure qui remplit les 15 premières lignes de la feuille de calcul avec les coefficients du triangle de Pascal :

2.3. Nombres parfaits

On dit qu'un nombre entier est parfait lorsqu'il est est égal à la somme de ses diviseurs. Ainsi par exemple, 28 est un nombre parfait car 28 = 1 + 2 + 4 + 7 + 14.

Écrire une fonction permettant de calculer la somme des diviseurs d'un entier quelconque, puis écrire une procédure qui détermine tous les entiers parfaits compris entre 1 et 10000.
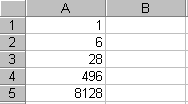
La copie d'écran ci-contre montre les 5 entiers parfaits que l'on trouvera ...

2.4. Anneaux olympiques (donné à la deuxième session 2000)

Placer un bouton marqué " Anneaux olympiques " sur la feuile de calcul et lui associer une procédure qui dessine les anneaux olympiques comme ci-dessous. Les différents anneaux (bleu, jaune, noir, vert et rouge) pourront avoir les propriétés suivantes (mais ce n'est pas obligatoire) :

• Rayon intérieur : 38
• Rayon extérieur : 47
• Centre de l'anneau bleu : (100, 100)
• Centre de l'anneau jaune : (200,100)
• Centre de l'anneau noir : (300, 100)
• Centre de l'anneau vert : (150, 150)
• Centre de l'anneau rouge : (250, 150).

La procédure associée au bouton fera elle-même appel à une procédure permettant de dessiner un anneau connaissant les coordonnées de son centre, ses rayons intérieur et extérieur et sa couleur.

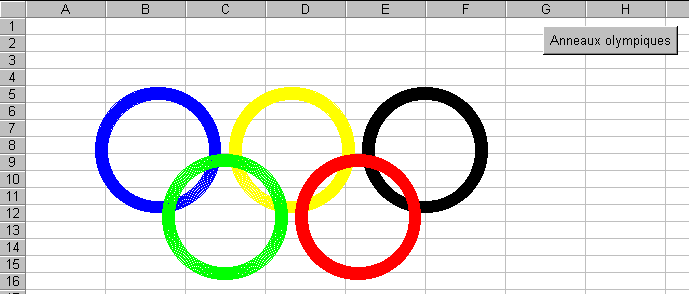
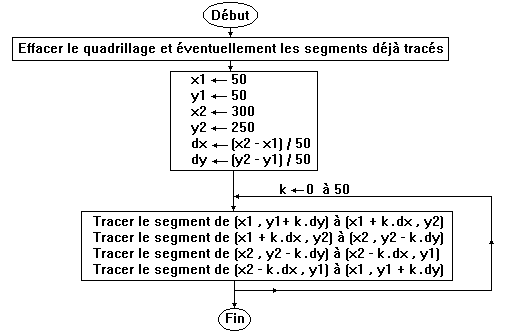
2.5. Tableau " pointes et fils "

Il s'agit de placer sur l'écran un bouton associé à une procédure qui réalise un joli dessin comme ceci :

Pour réaliser ce dessin, la procédure utilisée pourra suivre l'algorithme ci-dessous :

<< TP précédent      TP suivant >>

Retour à la liste des TP