Document sans titre

VISUAL BASIC & EXCEL

TP 7

Jeu de la Vie
(simulation de l'évolution d'une population bactérienne)

1. Solutions des exercices du TP 6

1.1. Fonction qui détermine si un nombre est premier ou non

Voici la solution décrite et expliquée pendant le TP de la semaine dernière :

Function EstPremier(n)
    If n < 4 Then
        EstPremier = True			'Les nombres entiers inférieurs à 4 sont premiers
    Else
        If n Mod 2 = 0 Then
            EstPremier = False	'Aucun nombre pair n'est premier
        Else
            k = 3						'On commence par essayer la division par 3
            Do While (k ^ 2 <= n) And (n Mod k > 0)
                k = k + 2			'k+2 est le diviseur potentiel suivant k
            Loop
            EstPremier = (k ^ 2 > n)
        End If
    End If
End Function

Remarque : Si cette fonction est placée dans la feuille de code associée à une feuille de calcul alors elle ne peut être utilisée que par une procédure de cette feuille de calcul. En revanche, si cette fonction est placée dans un module alors elle peut être utilisée depuis n'importe quelle feuille de code et même directement depuis une feuille de calcul comme étant une fonction définie par l'utilisateur ... On peut dans ce cas placer dans la cellule B1 (par exemple) la formule : = EstPremier(A1).

1.2. Test de la fonction EstPremier

Ce petit test n'a d'intérêt que parce qu'il montre comment remplir les 10 premières cellules des 10 premières lignes avec les 100 premiers nombres entiers :

Sub Test()
    Range("A1:J10").Clear
    For L = 1 To 10
        For C = 1 To 10
            Cells(L, C) = 10 * (L - 1) + C
            If EstPremier(Cells(L, C)) Then
                Cells(L, C).Interior.ColorIndex = 3
            End If
        Next C
    Next L
End Sub

1.3. Remplir 100 cellules de la colonne A et colorier ceux qui sont premiers

La solution ne présente aucune difficulté particulière. Nous avons simplement rajouté une variable nommée " Compteur " qui calcule au fur et à mesure du déroulement le nombre de nombres premiers :

Sub CentEntiers()
    Compteur = 0
    Range(Cells(1, 1), Cells(100, 1)).Clear
    Randomize
    For n = 1 To 100
        Cells(n, 1) = Int(1000 * Rnd + 1)
        If EstPremier(Cells(n, 1)) Then
            Range(Cells(n, 1), Cells(n, 1)).Interior.ColorIndex = 3
            Compteur = Compteur + 1
        End If
    Next
    Cells(1, 3) = "Il y a " & Str(Compteur) & " nombres premiers parmi ces 100 entiers"
End Sub

On aura remarqué, à la fin, comment on peut afficher un texte comportant une valeur numérique. Pour pouvoir accoler (on dit " concaténer ") 2 bouts de textes, on utilise l'opérateur de concaténation '&'. La fonction Str permet de transformer un nombre en une chaîne de caractères.

1.4. Recherche de tous les nombres premiers compris entre 2 entiers donnés a et b

Pas de difficulté particulière. On notera simplement comment on peut forcer l'utilisateur à entrer un deuxième nombre supérieur au premier (boucle Do.. loop until) :

Sub AfficherPremiers()
    Range(Cells(1, 1), Cells(1000, 1)).Clear
    a = InputBox("Entrer un entier a", "Recherche de nombres premiers")
    a = Val(a)
    Do
        b = InputBox("Entrer un entier b " & "(supérieur à " & Str(a) & ")", _
             "Recherche de nombres premiers")
        b = Val(b)
    Loop Until b > a
    Compteur = 0
    For n = a To b
        If EstPremier(n) Then
            Compteur = Compteur + 1
            Cells(Compteur, 1) = n
        End If
    Next
    Cells(1, 3) = "Il y a " & Str(Compteur) & " nombres premiers entre " & Str(a) & " et " & Str(b)
End Sub

Les lignes :

a = Val(a)
b = Val(b)

sont obligatoires car, sinon, la fonction InputBox retourne une chaîne de caractères ...

1.5. Solution du premier exercice de l'examen de juin 2001

Sub Pythagore2()    'entiers a,b,c,e tels que a^2 + b^2 + c^2 = e^2
    Cells.Clear
    n = 1           'n correspond au n° de la ligne d'affichage				
    For a = 1 To 98
        For b = a To 99
            For c = b To 100
                d = a * a + b * b + c * c
                e = Int(Sqr(d))					'e=partie entière de la racine de d 
                If e * e = d Then
                    Cells(n, 1) = a
                    Cells(n, 2) = b
                    Cells(n, 3) = c
                    Cells(n, 4) = d
                    Cells(n, 5) = e
                    n = n + 1
                End If
            Next
        Next
    Next
    Cells(1, 6) = (n - 1) & " solutions"
End Sub

1.6. Solution du second exercice de l'examen de juin 2001

Le second exercice était plus difficile, mais nous avions fait en TP quelque chose de semblable. Voici une première solution :

Sub Losange(x, y, hauteur, largeur, clBord, clIntérieur)
    With ActiveSheet.Shapes.BuildFreeform(msoEditingCorner, x, y - hauteur / 2)
        .AddNodes msoSegmentLine, msoEditingAuto, x - largeur / 2, y
        .AddNodes msoSegmentLine, msoEditingAuto, x, y + hauteur / 2
        .AddNodes msoSegmentLine, msoEditingAuto, x + largeur / 2, y
        .AddNodes msoSegmentLine, msoEditingAuto, x, y - hauteur / 2
        Set CeLosange = .ConvertToShape
    End With
    With CeLosange
        .Line.ForeColor.SchemeColor = clBord
        If clIntérieur >= 0 Then
            .Fill.Transparency = 0
            .Fill.ForeColor.SchemeColor = clIntérieur
            .Fill.OneColorGradient msoGradientHorizontal, 1, 1
        Else
            .Fill.Transparency = 1
        End If
    End With
End Sub

Sub Logo()
    x = 100
    y = 100
    ActiveSheet.DrawingObjects.Delete
    For hauteur = 130 To 101 Step -1
        largeur = 70 * hauteur / 100
        Losange x, y, hauteur, largeur, 0, -1
    Next
    Losange x, y, 100, 70, 0, 4
End Sub

Cette année, nous n'avons pas vu la construction de formes libres avec BuildFreeForm mais nous avons en revanche vu comment utiliser la méthode Polyline pour construire un triangle (cf. TP4). Voici donc une procédure équivalente pour définir un losange :

Sub Losange(x, y, hauteur, largeur, clBord, clIntérieur)
    Dim Sommet(1 To 5, 1 To 2) As Single
    Sommet(1, 1) = x
    Sommet(1, 2) = y - hauteur / 2
    Sommet(2, 1) = x - largeur / 2
    Sommet(2, 2) = y
    Sommet(3, 1) = x
    Sommet(3, 2) = y + hauteur / 2
    Sommet(4, 1) = x + largeur / 2
    Sommet(4, 2) = y
    Sommet(5, 1) = x                    'le 5ème sommet est confondu avec le 1er
    Sommet(5, 2) = y - hauteur / 2      'le 5ème sommet est confondu avec le 1er
    Set polygone = ActiveSheet.Shapes.AddPolyline(Sommet)
    polygone.Line.ForeColor.SchemeColor = clBord
    If clIntérieur >= 0 Then
        polygone.Fill.Transparency = 0
        polygone.Fill.ForeColor.SchemeColor = clIntérieur
        polygone.Fill.OneColorGradient msoGradientHorizontal, 1, 1
    Else
        polygone.Fill.Transparency = 1
    End If
End Sub

1.7. Solution du 3ème exercice de l'examen de juin 2001

Le joli napperon était spectaculaire mais facile à réaliser pour peu qu'on comprenne l'organigramme qui était proposé. En réalité , même si on ne comprend pas l'aspect mathématique de la construction, on peut quand même faire l'exercice en suivant pas à pas l'organigramme.

Voici le programme :

Const pi = 3.141592656
Sub napperons()
    ActiveSheet.DrawingObjects.Delete
    n = 30
    x0 = 170
    y0 = 170
    r = 170
    For i = 0 To n - 2
        Ti = 2 * i * pi / n
        a = x0 + r * Cos(Ti)
        b = y0 + r * Sin(Ti)
        For j = i + 1 To n - 1
            Tj = 2 * j * pi / n
            c = x0 + r * Cos(Tj)
            d = y0 + r * Sin(Tj)
            ActiveSheet.Shapes.AddLine a, b, c, d
        Next
    Next
End Sub

2. Jeu de la Vie : simulation de l'évolution d'une population bactérienne

L'un des premiers programmes qui essayait de simuler le processus d'expansion de la vie était "Life" de J. Conway en octobre 1970.
Le principe de base de ces programmes consiste à calculer les générations successives en partant d'une population initiale.
Notre population initiale sera représentée par les cellules de la feuille de calcul 1. Nous utiliserons des cellules très petites et chaque cellule pourra contenir une bactérie. La présence d'une bactérie sera matérialisée par la couleur rouge. Les règles suivantes déterminent la naissance, la survie ou la mort d'une bactérie :

Chaque bactérie ayant 2 ou 3 voisines survit pour la génération suivante.

Chaque bactérie ayant 4 voisines ou plus meurt par surpopulation.

Chaque bactérie n'ayant qu'une voisine ou aucune voisine meurt d'isolement.

Chaque cellule vide entourée exactement de 3 bactéries donne naissance à une nouvelle bactérie.

La marche à suivre est la suivante :

Il faut commencer par dimensionner manuellement les cellules. On pourra choisir, par exemple, de donner aux 50 premières colonnes (de A à AX) la largeur 0,4 puis on pourra donner aux 50 premières lignes la hauteur 4.0

Définir, dans une feuille de module, la procédure Infecter permettant d'ensemencer, de façon aléatoire, les cellules. Cette procédure pourra ressembler à ceci :
'Jeu de la vie

Const MaxL = 20
Const MaxC = 20

Sub Infecter()
    Range(Cells(2, 2), Cells(1 + MaxL, 1 + MaxC)).Clear
    Randomize
    For i = 1 To 100
        l = 2 + Int(MaxL * Rnd)
        c = 2 + Int(MaxC * Rnd)
        Cells(l, c).Interior.ColorIndex = 3
    Next i
End Sub
Les constantes MaxL et MaxC peuvent être facilement modifiées. Elles désignent le nombre de lignes et de colonnes atteintes par l'infection. La méthode Randomize permet d'initialiser le générateur de nombres aléatoires. La fonction Rnd fournit un nombre réel aléatoire compris entre 0 et 1. Nous multiplions ce nombre par MaxL. Il devient alors compris entre 0 et MaxL (exclus). Puis nous en prenons la partie entière (fonction Int) ce qui fournit un entier compris entre 0 et MaxL-1. Enfin nous ajoutons 2, ce qui donne un entier l compris entre 2 et MaxL+1. Même démarche pour le calcul de c. Notre population sera donc comprise dans le rectangle dont le bord supérieur gauche est cells(2,2) et dont le bord inférieur droit est cells(1+MaxL, 1+MaxC). Nous choisissons d'infecter une centaine de cellules. Par la suite, nous pourrons modifier ce nombre.

c. Ajouter, dans la feuille de calcul un bouton permettant de lancer la procédure Infecter.

d. Il s'agit maintenant de créer une procédure qui calcule la génération suivante de bactéries. Le principe général est le suivant :

On commence par effectuer un balayage de la zone infectée et chaque cellule rouge est remplie avec le nombre 1, chaque cellule blanche est remplie avec le nombre 0. Le fait que les cellules soient très petites entraîne que les nombres 1 ou 0 ne sont pas visibles.

On refait alors un deuxième balayage de la zone infectée et, pour chaque cellule, on compte le nombre de cellules voisines contenant une bactérie (chaque cellule possède 8 cellules voisines). Ce nombre de voisines infectées pourra être calculé par une fonction que l'on définira et qui additionnera les nombres contenus dans les cellules voisines. Selon que la cellule en cours de calcul est rouge ou blanche et selon le nombre de voisines infectées, on détermine sa nouvelle couleur. (voir les règles énoncées précédemment).

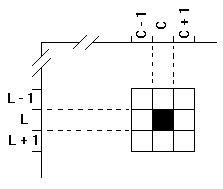
La cellule de coordonnées (L, C) et ses 8 voisines

L'écran pourra ressembler à ceci :

3. Suite de Syracuse

3.1. Définition d'une suite de Syracuse

On appelle Suite de Syracuse toute suite (u_n) d'entiers définie par son premier terme u₀ et par la relation de récurrence :

- si un est impair, alors u_n+1 = 3u_n + 1
- si un est pair, alors u_n+1 = u_n / 2.

Cette suite a été découverte vers 1970 et possède de nombreuses propriétés non encore démontrées (à ma connaissance). En particulier, il semble que toute suite de Syracuse soit périodique à partir d'un certain rang : la période est 3 et, à partir d'un certain rang qui dépend du premier terme, on obtient ...4, 2, 1, 4, 2, 1, 4, 2, 1 ...

Par exemple, la suite de Syracuse dont le premier terme est 51 est :

51, 154, 77, 232, 116, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1 ...

De même, la suite de Syracuse qui commence par 33 est :

33, 100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1 ...

Celle qui commence par 24 est : 24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1 ...

On le voit, le nombre de termes qui précèdent la partie périodique de la suite est variable et imprévisible. Cette première partie de la suite sera appelée partie apériodique de la suite.

3.2 Calculs

Écrire un programme qui permette d'obtenir un écran comme celui-ci :

L'utilisateur entre, dans la première ligne, des nombres entiers qui serviront de départ à des suites de Syracuse disposées en colonnes. Pour lancer les calculs on pourra utiliser la procédure suivante :
Sub Calculs()
    Range("A1,Z500").clear
    For c = 1 to 10
        If Cells(1, c) > 0 then Syracuse (c)
    next c
End Sub
La procédure Calculs fait appel à une procédure nommée Syracuse. C'est cette procédure qui devra permettre de calculer et d'afficher dans la colonne c les termes de la suite de Syracuse en arrêtant les calculs dès que le terme est égal à 1.

Déterminer l'entier n compris entre 1 et 100 qui donne la suite la plus longue ...

<< TP précédent TP suivant >>

Retour à la liste des TP