Document sans titre

VISUAL BASIC & EXCEL

TP 6

Nombres premiers, Exercices d'annales

1. Solution du jeu de Master Mind

1.1. Solution simple

Voici la solution complète, telle que nous l'avions finalisée la semaine dernière :

'Master Mind - Version simple
'TP 5 - ICES mars 2002

Sub Initialiser()
    Rows(1).Font.ColorIndex = 2     'couleur des caractères blanc sur fond blanc
    Rows(20).Font.ColorIndex = 2    'idem pour la ligne 20 qui contient une copie de la ligne 1
    Range("A1:K16").ClearContents
    Randomize
    For i = 1 To 5
        Cells(1, i) = Int(8 * Rnd)
    Next i
End Sub

Function CouleursBienPlacées(n)
    Résultat = 0
    For k = 1 To 5
        If Cells(1, k) = Cells(n, k) Then Résultat = Résultat + 1
    Next
    CouleursBienPlacées = Résultat
End Function

Function CouleursBienChoisies(n)
    Résultat = 0
    For k = 1 To 5
        Cells(20, k) = Cells(1, k)
    Next
    For k = 1 To 5
        Trouvé = False
        For i = 1 To 5
            If Not Trouvé _
                And Cells(n, k) = Cells(20, i) _
                And Cells(n, k) <> Cells(20, k) _
                And Cells(n, i) <> Cells(20, i) Then
                   Trouvé = True
                   Cells(20, i) = ""
                   Résultat = Résultat + 1
            End If
        Next i
    Next k
    CouleursBienChoisies = Résultat
End Function


Sub Calculs()
    n = ActiveCell.Row
    Cells(n, 7) = CouleursBienPlacées(n)
    Cells(n, 8) = CouleursBienChoisies(n)
End Sub

Sub Abandon()
    Rows(1).Font.ColorIndex = 1 'on remet la couleur des caractères en noir
End Sub

1.2. Une solution plus proche du jeu réel

Le jeu réel se joue avec des pions de couleurs (8 couleurs possibles). On peut simuler un pion coloré par le caractère pris dans la police Wingdings par exemple.

Pour commencer, on remplit la cellule A1, manuellement, avec ce caractère, de taille assez grande et de couleur blanc pour qu'il ne se voit pas à l'affichage. On précise ensuite que ce caractère doit être centré dans la cellule, tant horizontalement que verticalement (Format / Cellules / Alignement). Enfin, on reproduit la cellule A1 jusqu'à la cellule E20.

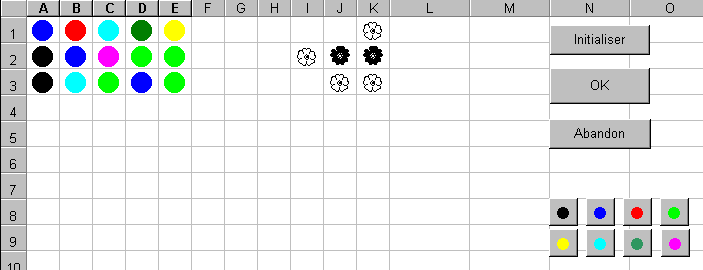
Voici ce qu'on obtient à l'écran (ici les pions sont visibles, mais, dans la réalité ils doivent être en blanc sur fond blanc) :

La colonne F servira à séparer les combinaisons essayées et les réponses affichées par l'ordinateur.

Les colonnes G, H, I, J et K serviront à afficher les réponses calculées par l'ordinateur. Dans le jeu réel, les réponses sont des petits pions : un pion noir pour chaque couleur bien placée et un pion blanc pour chaque couleur bien choisie mais mal placée.
On peut remplacer ces pions par les caractères Wingdings et . Il faut donc préciser que les cellules de la zone G1 à K20 seront formatées avec cette police avec une taille asez grande (format / cellules / police). De plus il convient encore une fois de centrer aussi bien verticalement qu'horizontalement. Pour le moment, ces cellules doivent rester vides : il s'agit seulement de régler leur format.

Voici le texte complet de la feuille de code :

'Master Mind - Version plus élaborée
'TP 5 - ICES mars 2002

Dim Combinaison(1 To 5) As Byte  'combinaison secrète à 5 positions

Function Couleur(Code)
    Select Case Code
        Case 1: Couleur = 1     'Noir
        Case 2: Couleur = 5     'Bleu
        Case 3: Couleur = 3     'Rouge
        Case 4: Couleur = 4     'Vert
        Case 5: Couleur = 6     'Jaune
        Case 6: Couleur = 8     'Cyan
        Case 7: Couleur = 10    'Vert foncé
        Case 8: Couleur = 7     'Violet
    End Select
End Function

Function Code(Couleur)
    Select Case Couleur
        Case 1: Code = 1     'Noir
        Case 5: Code = 2     'Bleu
        Case 3: Code = 3     'Rouge
        Case 4: Code = 4     'Vert
        Case 6: Code = 5     'Jaune
        Case 8: Code = 6     'Cyan
        Case 10: Code = 7    'Vert foncé
        Case 7: Code = 8     'Violet
    End Select
End Function

Sub Initialiser()
    Range("A1:E20").Font.ColorIndex = 2     'on masque les pions en mettant en blanc
    Range("F1:K20").ClearContents           'on efface les réponses de la partie précédente
    Randomize
    For k = 1 To 5
        Combinaison(k) = Int(8 * Rnd) + 1
    Next k
End Sub

Function CouleursBienPlacées(n)
    Résultat = 0
    For k = 1 To 5
        If Code(Cells(n, k).Font.ColorIndex) = Combinaison(k) Then
            Résultat = Résultat + 1
        End If
    Next
    CouleursBienPlacées = Résultat
End Function

Function CouleursBienChoisies(n)
    Résultat = 0
    For k = 1 To 5
        Cells(20, k) = Combinaison(k)
    Next
    For k = 1 To 5
        Trouvé = False
        For i = 1 To 5
            If Not Trouvé _
                And Code(Cells(n, k).Font.ColorIndex) = Cells(20, i) _
                And Code(Cells(n, k).Font.ColorIndex) <> Cells(20, k) _
                And Code(Cells(n, i).Font.ColorIndex) <> Cells(20, i) Then
                Trouvé = True
                Cells(20, i) = ""
                Résultat = Résultat + 1
            End If
        Next i
    Next k
    CouleursBienChoisies = Résultat
End Function

Sub Calculs()
    n = ActiveCell.Row
    bp = CouleursBienPlacées(n)
    bc = CouleursBienChoisies(n)
    For k = 1 To 5
        Cells(n, 5 + k) = ""		'On commence par effacer les cellules réponses de la ligne n
    Next k
    For k = 1 To bp
        Cells(n, 12 - k) = "|"	'Le caractère | correspond au caractère Wingdings de code 124
    Next k
    For k = 1 To bc
        Cells(n, 12 - bp - k) = "{"	'De même le caractère { représente a pour code 123
    Next k
End Sub

Sub Abandon()
    For k = 1 To 5
        Cells(19, k).Font.ColorIndex = Couleur(Combinaison(k))
    Next k
End Sub

'Suivent maintenant 8 procédures qui correspondent aux 8 boutons permettant de choisir les pions de
'différentes couleurs :


Sub btNoir()
    ActiveCell.Font.ColorIndex = 1
End Sub

Sub btBleu()
    ActiveCell.Font.ColorIndex = 5
End Sub

Sub btRouge()
    ActiveCell.Font.ColorIndex = 3
End Sub

Sub btVert()
    ActiveCell.Font.ColorIndex = 4
End Sub


Sub btJaune()
    ActiveCell.Font.ColorIndex = 6
End Sub

Sub btCyan()
    ActiveCell.Font.ColorIndex = 8
End Sub

Sub btVertFoncé()
    ActiveCell.Font.ColorIndex = 10
End Sub

Sub btViolet()
    ActiveCell.Font.ColorIndex = 7
End Sub

La combinaison secrète est toujours, en interne, une combinaison de 5 chiffres choisis parmi les chiffres de 1 à 8. Il est donc nécessaire d'écrire 2 fonctions : la première permet de traduire chaque chiffre en une couleur et la seconde fait le contraire. Dans notre exemple les couleurs retenues sont noir, bleu, rouge, vert, jaune, cyan, vert foncé et violet. Ces couleurs ont respectivement pour codes 1, 5, 3, 4, 6, 10, 8 et 7.

On trouvera, en haut de la page suivante, un début de partie.

On remarquera, en particulier, les 8 boutons de couleurs : il suffit de choisir, comme texte de chacun de ces boutons, le caractère et de le mettre dans la couleur correspondant à la fonction du bouton.

2. Exercices sur les nombres premiers

Les nombres premiers ont toujours fasciné les mathématiciens depuis l'antiquité. Rappelons qu'un nombre entier naturel est premier lorsqu'il ne possède pas d'autres diviseurs que 1 et lui-même. La suite des nombres premiers est infinie. Le début de cette suite est : 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ...

2.1. Écriture d'une fonction qui détermine si un entier est premier ou non

Il s'agit d'écrire une fonction EstPremier(n) qui retourne la valeur VRAI si n est un entier naturel premier, FAUX si n est un entier naturel non premier.
Voici l'organigramme de cette fonction, basé sur un algorithme très simple :

2.2. Test de la fonction EstPremier

Pour tester la fonction EstPremier, écrire un programme qui remplit les cellules des 10 premières lignes et 10 premières colonnes avec les nombres entiers de 1 à 100 et qui met la cellule sur fond rouge lorsqu'il s'agit d'un entier premier.
Voici l'écran qu'on doit obtenir :

Pour remplir les 100 cellules avec les entiers de 1 à 100, il suffit de faire 2 boucles imbriquées l'une dans l'autre :

2.3. Exercices

Écrire une procédure qui remplit les 100 premières cellules de la colonne A par des nombres entiers aléatoires compris entre 1 et 1000 et mettre le fond des cellules contenant un entier premier en rouge.

Écrire un procédure qui demande à l'utilisateur d'entrer un entier a, puis un entier b (b>a), puis qui affiche, dans la colonne A, tous les nombres premiers compris entre a et b.

3. Exercices d'annales (Session de juin 2001)

3.1. Exercice 1

Définir une procédure qui affiche tous les quadruplets (a, b, c, e) de nombres entiers tels que a² + b² + c² = e² et 1 £ a £ b £ c £ 100.
Les colonnes A, B, C, D et E contiendront respectivement les entiers a, b, c, a² + b² + c² et e.
Un bouton permettra de lancer l'exécution de la procédure.
La cellule F1 contiendra le nombre de solutions.

On obtiendra à l'écran, quelque chose comme ceci (on ne voit ici que les 18 premières solutions) :

3.2. Exercice 2

Le but de cet exercice est d'obtenir le dessin ci-dessous composé d'un losange épais dont les côtés sont de couleur noire et l'intérieur de couleur vert dégradé. Pour obtenir l'aspect dégradé, on pourra se servir d'un exemple donné au TP4.

La procédure principale sera la suivante :
Sub Logo()
    x = 100
    y = 100
    ActiveSheet.DrawingObjects.Delete
    For hauteur = 130 To 101 Step -1
        largeur = 70 * hauteur / 100
        Losange x, y, hauteur, largeur, 0, -1
    Next
    Losange x, y, 100, 70, 0, 3
End Sub
Cette procédure, nommée Logo, fait appel elle-même à une procédure nommée Losange qu'il s'agit de définir. L'en-tête de cette procédure sera la suivante :

Sub Losange(x, y, hauteur, largeur, clBord, clIntérieur)

Les différents paramètres sont définis ainsi :

x abscisse du centre du losange

y ordonnée du centre du losange

hauteur hauteur du losange

largeur largeur du losange

clBord couleur des côtés du losange (la couleur 0 correspond au noir)

clIntérieur couleur intérieure du losange. Si cette couleur est négative, on considère que le losange est transparent. Le code de la couleur verte est 3.

3.3. Exercice 3

L'objectif est de dessiner le " napperon " ci-dessous :

Pour réaliser ce dessin, on pourra suivre l'organigramme ci-contre :

<< TP précédent TP suivant >>

Retour à la liste des TP

x	abscisse du centre du losange
y	ordonnée du centre du losange
hauteur	hauteur du losange
largeur	largeur du losange
clBord	couleur des côtés du losange (la couleur 0 correspond au noir)
clIntérieur	couleur intérieure du losange. Si cette couleur est négative, on considère que le losange est transparent. Le code de la couleur verte est 3.