Document sans titre

VISUAL BASIC & EXCEL

TP 5

Jeu de Master Mind®

1. Solutions des exercices du TP4

1.1. Carré magique " en diagonale vers le nord-ouest "

'Carrés magiques impairs
'TP 4 - ICES Mars 2002

Sub CarréMagique()
    Do
        n = InputBox("Entrez un entier impair inférieur à 100", "Carré magique")
        n = Val(n)
        
        'la fonction InputBox retourne une chaîne de caractères. Il est donc
        'nécessaire de traduire cette chaîne en un nombre, ce que fait la fonction Val
        
    Loop Until (n Mod 2 = 1) And (n < 100)
    
    Range(Cells(1, 1), Cells(100, 100)).ClearContents
    
    'ClearContents n'efface que les données, pas les formats. Ainsi, si
    'on a défini le format des cellules en centrant leur contenu, la méthode
    'Clear efface tout (contenu et format), ce qui n'est pas le cas de ClearContents
    
    a = (n + 1) / 2
    b = (n - 1) / 2
    For x = 1 To n * n
        Cells(a, b) = x
        If x Mod n = 0 Then
            b = b - 2
        Else
            a = a - 1
            b = b - 1
        End If
        If a < 1 Then a = a + n
        If b < 1 Then b = b + n
    Next
End Sub

1.2. Carré magique " en diagonale vers le nord-est "

'Carrés magiques impairs remplis différemment
'TP 4 - ICES Mars 2002

Sub CarréMagique2()
    Do
        n = InputBox("Entrez un entier impair inférieur à 100", "Carré magique")
        n = Val(n)
    Loop Until (n Mod 2 = 1) And (n < 100)
    Range(Cells(1, 1), Cells(100, 100)).ClearContents
    a = (n + 1) / 2
    b = (n + 3) / 2
    For x = 1 To n * n
        Cells(a, b) = x
        If x Mod n = 0 Then
            b = b + 2
        Else
            a = a - 1
            b = b + 1
        End If
        If a < 1 Then a = a + n
        If b > n Then b = b - n
    Next
End Sub

1.3. Fonction " PlusGrandDiviseurDe "

La structure principale de l'organigramme correspond à une boucle " Do Until...Loop " :

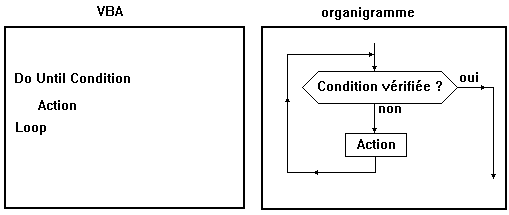
Le programme qui en découle est donc très simple :

'Fonction 'PlusGrandDiviseurDe'
'TP 4 - ICES Mars 2002

Function PlusGrandDiviseurDe(n)
    d = n \ 2			'le premier diviseur essayé est d=partie entière de d/2
    Do Until n Mod d = 0	'Répéter jusqu'à ce que n soit multiple de d
        d = d - 1
    Loop
    PlusGrandDiviseurDe = d
End Function

1.4. Fonction " DécomposeEnFacteursPremiers "

L'organigramme est plus compliqué. Il contient 2 boucles de type Do...Loop.

La première boucle est la suivante :

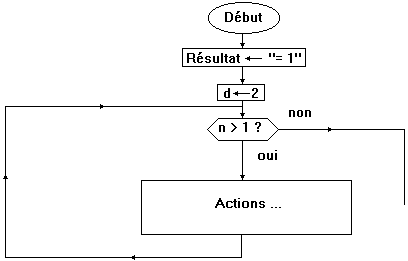
D'après le cours, il s'agit d'une boucle de type " Do While ... Loop "

Le début du programme est donc :

Function DécomposeEnFacteursPremiers(n)
    Résultat = "= 1"
    d = 2
    Do While n > 1

La seconde boucle se trouve à l'intérieur de la première :

D'après le cours, il s'agit d'une boucle " Do Until ... Loop "

Le programme complet est donc :

'Fonction 'DécomposeEnFacteursPremiers'
'TP 4 - ICES Mars 2001

Function DécomposeEnFacteursPremiers(n)
    Résultat = "= 1"
    d = 2
    Do While n > 1
        Do Until n Mod d = 0
            d = d + 1
        Loop
        Résultat = Résultat & " x " & d
        n = n \ d
    Loop
    DécomposeEnFacteursPremiers = Résultat
End Function

2. Jeu de Super MasterMind®

2.1. Règle du jeu

Il s'agit d'un célèbre jeu de stratégie. Il se joue à 2 joueurs :

Le premier joueur fabrique une combinaison secrète de 5 couleurs choisies parmi 8 couleurs. Le code secret peut comporter plusieurs fois la même couleur.

Le second joueur cherche, par tâtonnements successifs, à trouver la combinaison secrète. Après chaque essai, le premier joueur donne 2 indications :

Le nombre de couleurs bien choisies, bien placées,

Le nombre de couleurs bien choisies mais mal placées.

L'objectif est de trouver la combinaison secrète en faisant le moins d'essais possibles.

2.2. Adaptation du jeu sur Excel

Pour simplifier, dans un premier temps, les couleurs seront remplacées par des chiffres compris entre 1 et 8.
C'est l'ordinateur qui va jouer le rôle du premier joueur.
L'ordinateur va devoir fabriquer 5 nombres entiers au hasard et les placer, de façon invisible, dans les 5 cellules A1, B1, C1, D1, E1. Pour que la combninaison ne soit pas visible du joueur, il suffira d'afficher celle-ci en blanc sur fond blanc.

Les colonnes A,B,C,D et E serviront, à partir de la ligne 2, à recevoir les essais du joueur (de l'utilisateur).
Les colonnes G,H,I,J et K serviront à l'ordinateur pour indiquer combien de couleurs sont bien choisies bien placées et combien de couleurs sont bien choisies mais mal placées.
Le nombre d'essais du joueur sera limité à 15.

Commencer par régler manuellement la largeur des colonnes A à K à 4 caractères.
Mettre l'alignement de ces 11 colonnes sur " centré ".

2.3. Initialisation

Écrire une procédure qui permet de :

Effacer la plage de cellules A1 à K16

Initialiser le générateur aléatoire (instruction Randomize)

Dans une boucle de type For, créer 5 nombres entiers aléatoires compris entre 1 et 8. Un tel nombre peut être défini par la séquence Int(8*Rnd)+1 exactement comme sur une calculatrice. Mettre ces nombres dans les cellules A1 à A5 en précisant que la couleur de l'affichage doit être blanc.

Ajouter un bouton permettant de lancer la procédure Initialisation. Pour vérifier que les entiers sont bien calculés et différents à chaque lancement, on pourra, dans un premier temps, les afficher en clair sur l'écran.

2.3. Introduction des essais

Dans un premier temps, les combinaisons sont des nombres à 5 chiffres et non pas des couleurs. Il n'y a donc rien à programmer : le joueur saisira directement ses essais dans la grille et, lorsqu'il jugera que son essai est correct, il devra cliquer sur un bouton qui lancera les calculs et permettra à l'ordinateur d'indiquer sa réponse.

2.4. Calcul des réponses

Toujours dans le but de simplifier la programmation, nous n'allons utiliser que 2 colonnes : G et H. La colonne G contiendra le nombre de chiffres corrects et bien placés dans l'essai. La colonne H contiendra le nombre de chiffres corrects mais mal placés. Le numéro de l'essai sera déterminé par le numéro de la ligne : si l'essai se trouve sur la ligne 5, alors il s'agit de l'essai n° 4. Au moment du clic sur le bouton qui lancera les calculs, il faudra que la cellule active soit sur la ligne de l'essai en cours de calcul.

Voici la procédure qui devra effectuer les calculs (à laquelle il faudra associer un bouton) :
Sub Calculs()
   n = ActiveCell.Row
   Cells(n , 7) = CouleursBienPlacées(n)
   Cells(n , 8) = CouleursBienChoisies(n)
End sub
Cette procédure remplit la cellule (n,7) (ligne n, colonne 7=G) avec le résultat de la fonction " CouleursBienPlacées " et la cellule (n, 8) avec le résultat de la fonction " CouleursBienChoisies ". Voici le code de la première fonction :
Function CouleursBienPlacées(n)
   Resultat = 0
   For k = 1 to 5
      If cells(1, k) = cells(n, k) then
         Resultat = Resultat + 1
      End if
   Next
   CouleursBienPlacées = Resultat
End function
La seconde fonction est beaucoup plus difficile à analyser : elle sera expliquée au cours du TP ...

<< TP précédent TP suivant >>

Retour à la liste des TP