Voici le texte complet :

'Procédures graphiques du TP3
'ICES-Deug SV2-Mars 2002

Sub Géométrie()
    Sheets("Feuil2").Activate
    ActiveWindow.DisplayGridlines = False
    ActiveSheet.DrawingObjects.Delete
    With Sheets("Feuil1")
    For i = 1 To 10
       Select Case .Cells(i, 1)
         Case "Segment"
             Segment .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5), _
                    .Cells(i, 6)
         Case "Rectangle"
             Rectangle .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5), _
                    .Cells(i, 6), .Cells(i, 7)
         Case "Ellipse"
             Ellipse .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5), _
                    .Cells(i, 6), .Cells(i, 7)
         Case "Triangle"
             Triangle .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5), _
                        .Cells(i, 6), .Cells(i, 7), .Cells(i, 8), .Cells(i, 9)
         Case "Cercle"
             Cercle .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), _
                    .Cells(i, 5), .Cells(i, 6)
         Case "DroiteAB"
             DroiteAB .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5), _
                    .Cells(i, 6)
       End Select
    Next
    End With
End Sub

Sub Segment(x1, y1, x2, y2, c)
    Set seg = ActiveSheet.Shapes.AddLine(x1, y1, x2, y2)
    seg.Line.ForeColor.SchemeColor = c
End Sub


Sub Rectangle(x1, y1, x2, y2, clBord, clInterieur)
    Set rect = ActiveSheet.Shapes.AddShape(msoShapeRectangle, x1, y1, x2 - x1, y2 - y1)
    rect.Fill.Transparency = 0
    rect.Fill.ForeColor.SchemeColor = clInterieur
    rect.Line.ForeColor.SchemeColor = clBord
End Sub

Sub Ellipse(x, y, rx, ry, clBord, clInterieur)
    x1 = x - rx: y1 = y - ry
    largeur = 2 * rx: hauteur = 2 * ry
    Set Ell = ActiveSheet.Shapes.AddShape(msoShapeOval, x1, y1, largeur, hauteur)
    Ell.Fill.Transparency = 0
    Ell.Fill.ForeColor.SchemeColor = clInterieur
    Ell.Line.ForeColor.SchemeColor = clBord
End Sub

Sub Triangle(x1, y1, x2, y2, x3, y3, clBord, clInterieur)
    Dim Sommet(1 To 4, 1 To 2) As Single
    Sommet(1, 1) = x1
    Sommet(1, 2) = y1
    Sommet(2, 1) = x2
    Sommet(2, 2) = y2
    Sommet(3, 1) = x3
    Sommet(3, 2) = y3
    Sommet(4, 1) = x1
    Sommet(4, 2) = y1
    Set Tri = ActiveSheet.Shapes.AddPolyline(Sommet)
    Tri.Fill.Transparency = 0
    Tri.Fill.ForeColor.SchemeColor = clInterieur
    Tri.Line.ForeColor.SchemeColor = clBord
    Tri.Fill.OneColorGradient msoGradientHorizontal, 1, 1
End Sub

Sub Cercle(x, y, r, clBord, clInterieur)
    Ellipse x, y, r, r, clBord, clInterieur
End Sub

Sub DroiteAB(xa, ya, xb, yb, c)
    x = xa
    y = ya
    dx = xb - xa
    dy = yb - ya
    Do While dx * dx + dy * dy > 10
        Do While x + dx > 0 And x + dx < 500 And y + dy > 0 And y + dy < 400
            x = x + dx
            y = y + dy
        Loop
        dx = dx / 2
        dy = dy / 2
    Loop
    x1 = x
    y1 = y

    x = xa
    y = ya
    dx = xa - xb
    dy = ya - yb
    Do While dx * dx + dy * dy > 10
        Do While x + dx > 0 And x + dx < 500 And y + dy > 0 And y + dy < 400
            x = x + dx
            y = y + dy
        Loop
        dx = dx / 2
        dy = dy / 2
    Loop
    x2 = x
    y2 = y
    Segment x1, y1, x2, y2, c
End Sub

2. Carrés magiques

Tout le monde connaît sans doute la définition d'un carré magique. Rappelons qu'un tel carré, de côté n, (n entier naturel non nul) contient les nombres entiers de 1 à n², disposés de telle sorte que :

• les sommes des nombres de chaque colonne,
• les sommes des nombres de chaque ligne,
• les sommes des nombres des deux diagonales,
  soient toutes égales.

Voici, par exemple, un carré magique de côté 3 :

Dans le cas de ce carré, toutes les colonnes, toutes les lignes et les 2 diagonales contiennent des entiers dont la somme est toujours 15.

La méthode que nous proposons, valable uniquement pour les carrés de côté impair, est particulièrement simple :

• nous notons a et b les n° de ligne de et de colonne. (avec 1£a£ n et 1£b£n)
• dans tous les carrés impairs, il y a une cellule centrale, de coordonnées
• on commence par remplir avec le chiffre 1, la cellule située juste à gauche de la cellule centrale.
• on continue ensuite à remplir les autres cases avec la suite des entiers jusqu'à n², en suivant les règles suivantes (montrées sur l'exemple du carré 11x11) :
  • d'une manière générale, on se déplace d'une case à la suivante, en choisissant (si elle existe) la cellule située en haut à gauche de la cellule courante.

  

  • si la cellule courante est située au bord gauche (si b = 1), alors considérer que la colonne la plus à droite touche la colonne la plus à gauche (prendre b = n). Voir le schéma page suivante.

  

  • si la cellule courante est située au bord supérieur (si a = 1), alors considérer que la ligne la plus basse touche la ligne la plus haute (prendre a = n)

  

  • si, malgré l'application des règles précédentes, la cellule suivante est déjà occupée, alors prendre la cellule de la même ligne, 2 colonnes plus à gauche.

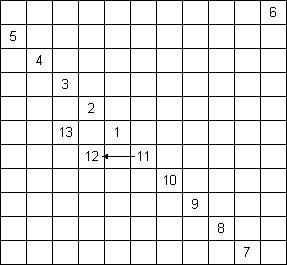
Voici, en résumé, l'organigramme décrivant la construction d'un carré magique impair selon cette méthode :

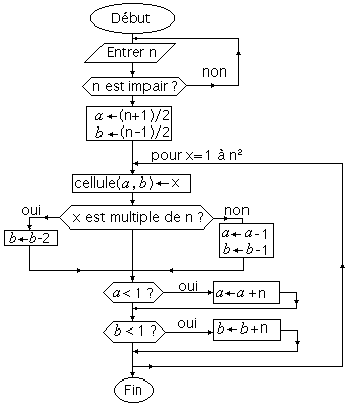
Pour bien comprendre cet organigramme, et pour le traduire en langage VBA, il faut expliquer les opérations qui permettent de déterminer si un nombre entier est impair ou si un nombre entier est un multiple d'un autre.

La phrase " n est impair " peut se traduire par : " la division de n par 2 ne tombe pas juste "
Ou bien par : " le reste de la division de n par 2 est > 0 "

La phrase " x est multiple de n " peut se traduire par : " la division de x par n tombe juste "
ou bien par : " le reste de la division de x par n est égal à 0 "

On le voit, dans les deux cas, la question revient à calculer le reste de la division d'un entier par un autre entier. Il existe pour cela, en langage VBA comme dans tous les langages informatiques (y compris les langages des calculatrices programmables), une opération binaire, (c'est-à-dire à 2 opérandes) qui calcule le reste d'une division. Cette opération s'appelle MOD.

Tout le monde connaît les 6 opérations binaires classiques :

• L'addition : 25 + 4 = 29
• La soustraction : 25 - 4 = 21
• La multiplication : 25 ´ 4 = 100 (notée * en VBA)
• La division : 25 ÷ 4 = 6,25 (notée / en VBA)
• L'exponentiation : 25 ^ 4 = 390 625
• L'exponentiation inverse : 25 Ö 4 = 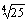= 2,236... (n'existe pas en VBA)

Il existe 2 autres opérations binaires très intéressantes :

• La division entière : 25 \ 4 = 6 (quotient entier de 25 par 4, noté parfois 25 div 4)
• Le reste de la division entière : 25 mod 4 = 1.

Grâce à cette nouvelle opération, il est très facile de déterminer si un nombre entier est impair ou si un entier est multiple d'un autre entier.

Commencer par définir les dimensions des 20 colonnes et des 20 premières lignes :

• Largeur des colonnes : 3 (caractères)
• Hauteur des lignes : 20 (points).

3. Exercices

3.1. Carré magique " à l'envers " (donné à l'examen de juin 1999)

En utilisant une méthode analogue à celle du TP4, écrire une procédure permettant de construire un carré magique de côté impair mais en considérant que les cellules seront remplies selon les règles suivantes :

• La cellule de départ est située à droite de la cellule centrale (et non pas à gauche),
• La cellule suivante, si elle est libre, est située au-dessus et à droite de la cellule actuelle (et non pas au-dessus et à gauche).
• Si la cellule au-dessus et à droite est occupée, alors la cellule suivante est située 2 cellules à droite.
  À titre d'exemple, voici le début de la construction du carré magique de 7 :

3.2. Fonction PlusGrandDiviseurDe

Il s'agit de créer une fonction qui calcule, pour un entier donné n, le plus grand diviseur de n autre que n lui-même.

Pour tester notre fonction, nous utiliserons la technique suivante : l'utilisateur entre dans les cellules de la colonne A des nombres entiers. Excel calcule alors, dans les cellules de la colonne B, le plus grand diviseur de ces nombres.

La marche à suivre est la suivante :

• Écrire la fonction PlusGrandDiviseurDe dans une feuille de module (pour cela, utiliser dans le menu Insertion de Visual Basic, la commande Insertion/Module)
• Remplir quelques cellules de la colonne A par des nombres entiers,
• Écrire, dans la cellule B1, la formule : = PlusGrandDiviseurDe(A1)
• Recopier cette formule vers le bas autant de fois que nécessaire.

À la fin, on doit avoir sur l'écran quelque chose comme ceci :

L'organigramme de cette fonction est le suivant :

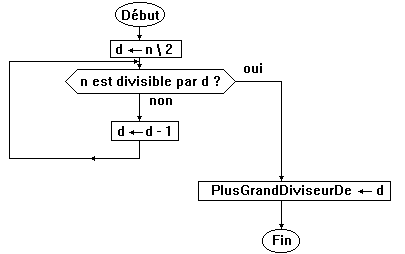
Remarque : noter la division de n par 2, au début, qui se fait avec la barre \ au lieu de / afin de faire une division entière et non pas une division réelle.

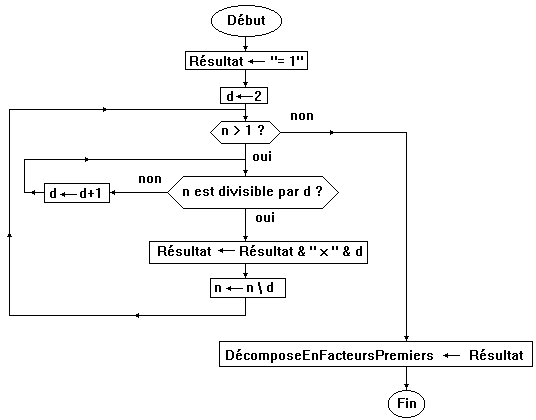
3.3. Fonction DécomposeEnFacteursPremiers

Selon les mêmes modalités que pour l'exercice précédent, l'utilisateur saisit des nombres entiers dans la colonne A et Excel décompose les nombres en un produit de facteurs premiers. Il s'agit cette fois, d'obtenir à l'écran à peu près ceci :

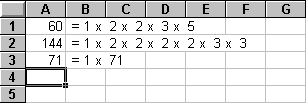
L'organigramme est le suivant :

<< TP précédent      TP suivant >>

Retour à la liste des TP