1.1. Solution (presque) sans programmation

Dans un premier temps, on peut se contenter de ne programmer que la fonction à étudier :

• Lancer Visual Basic Editor (Outils / Macro / Visual Basic Editor)
• Faire la commande Insertion / Module (pour que la fonction ainsi définie soit directement accessible depuis la feuille de calcul, il faut qu'elle soit placée dans un Module)
• Il suffit alors de taper la définition de la fonction, comme ceci par exemple :

   

  Function f(x)
     f = 1 / (x ^ 2 + 1)
  End Function

  

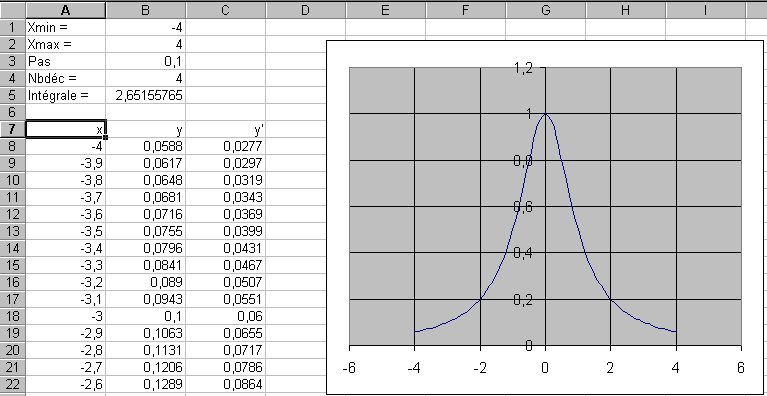
Les cellules B1, B2, B3 et B4 sont respectivement nommées Xmin, Xmax, Pas et NbDéc et sont initialisées avec des valeurs quelconques.
La cellule A8 contient la formule : =Xmin
La cellule B8 contient la formule : =SI(A8="","",ARRONDI(f(A8),Nbdéc))
La cellule C8 contient la formule plus compliquée :

=SI(A8="","",(SI(ET(f(A8)<>"",f(A8+0.00001)<>""),ARRONDI((f(A8+0.00001)-f(A8))/0.00001,Nbdéc))))

La cellule A9 contient la formule :
=SI(A8="","",SI(A8+Pas<=Xmax,ARRONDI(A8+Pas,Nbdéc),""))
Il suffit alors de recopier vers le bas autant que nécessaire (au moins sur une centaine de lignes), les formules A9, B8 et C8.
Enfin, la cellule B5 contient la formule : =(SOMME(B8:B100)-f(Xmax))*Pas

Pour obtenir la courbe représentative, il faut impérativement sélectionner les cellules des colonnes A et B, à partir de la ligne 8 jusqu'à la valeur de Xmax puis utiliser l'assistant graphique et suivre la procédure décrite dans le TP2.

L'inconvénient de cette méthode est que si nous changeons les bornes et/ou le pas, alors le graphique ne sera plus adapté à la nouvelle fonction au niveau de la zone sélectionnée.

1.2. Solution plus complète

La solution ci-dessous fait à peu près la même chose mais, d'une part, l'intégrale est calculée de façon plus sûre, indépendamment du choix du pas et de l'intervalle, et d'autre part, le graphique s'adapte automatiquement au changement de fonction, d'intervalle et de pas.

Pour permettre l'étude de n'importe quelle fonction, même si on ne connaît pas son domaine de définition (ou si on n'a pas envie de le chercher ce qui revient au même), on peut utiliser la technique ci-dessous :

Function f(x)    On Error Goto Erreur       f = Sqr(1 - x ^ 2)    Exit Function Erreur:    f = ""    Resume Next End Function

Si une erreur se produit aller à Erreur    Calcul de f(x) On quitte alors la fonction S'il y a eu une erreur, alors f = rien Retour du programme après l'instruction qui a provoqué l'erreur (retour à Exit Function)

Dans cette méthode, l'instruction " Exit function " est indispensable car, sinon, le programme se poursuivrait et f serait alors toujours égal à " rien ".

'Solution du TP2 ICES SV2 2002

Function f(x)
    On Error GoTo Erreur
        f = 1 / (x ^ 2 + 1)  'c'est ici qu'on peut changer la fonction
    Exit Function
    
Erreur:
    f = ""
    Resume Next
End Function

Function Intégrale(XMin, XMax)
'calcul de l'intégrale de f(x)dx de XMin jusqu'à XMax
'le calcul reste correct même si XMax<Xmin
    i = 0
    x = XMin
    dx = (XMax - XMin) / 100 'dx est négatif lorsque XMin>xMax
    Do
        i = i + f(x) * dx
        x = x + dx
    Loop While (dx > 0 And x < XMax) Or (dx < 0 And x > XMax)
    'la condition ci-dessus tient compte des 2 cas possibles
    
    Intégrale = i
End Function

Sub Graphique(XMin, XMax, Pas)
    ActiveSheet.ChartObjects.Delete
    ActiveSheet.ChartObjects.Add(200, 30, 350, 250).Select
    ActiveChart.ChartWizard Source:= _
        Range(Cells(8, 1), Cells(8 + (XMax - XMin) / Pas, 2)), _
        gallery:=xlXYScatter, Format:=6, PlotBy:=xlColumns, _
        categorylabels:=1, serieslabels:=0, HasLegend:=False
End Sub

Sub calculs()
    Range(Cells(8, 1), Cells(500, 3)).Clear
    XMin = Cells(1, 2)
    XMax = Cells(2, 2)
    Pas = Cells(3, 2)
    
    If Pas > 0 And XMax < XMin Then
        MsgBox ("Erreur : le pas est positif et XMax<XMin")
        Exit Sub
    End If
    
    If Pas < 0 And XMax > XMin Then
        MsgBox ("Erreur : le pas est négatif et XMax>XMin")
        Exit Sub
    End If
        
    nbdéc = Cells(4, 2)
    ch = "0."
    For i = 1 To nbdéc
        ch = ch & "0"
    Next i
    Range(Cells(8, 1), Cells(500, 3)).NumberFormat = ch
    i = 8
    x = XMin
    Do While (x <= XMax + 0.0000001 And Pas > 0) _
            Or (x >= XMax - 0.0000001 And Pas < 0)
        Cells(i, 1) = x
        Cells(i, 2) = f(x)
        If f(x) <> "" And f(x + 0.00001) <> "" Then
            Cells(i, 3) = (f(x + 0.00001) - f(x)) / 0.00001
        Else
            Cells(i, 3) = ""
        End If
        x = x + Pas
        i = i + 1
    Loop
    Cells(5, 2) = Intégrale(XMin, XMax)
    Graphique XMin, XMax, Pas
End Sub

On notera que, dans le texte ci-dessus, les bornes Xmin et Xmax peuvent être inversées, à condition de choisir un pas négatif lorsque Xmax est inférieur à Xmin : dans ce cas, si la fonction est positive, l'intégrale sera négative...

La procédure graphique est assez compliquée :

• D'abord, on commence par effacer les graphiques précédents (indispensable si on lance plusieurs fois les calculs, sinon, les graphiques se superposent les uns aux autres et la feuille devient rapidement illisible). Ceci est réalisé par l'instruction ActiveSheet.ChartObjects.Delete
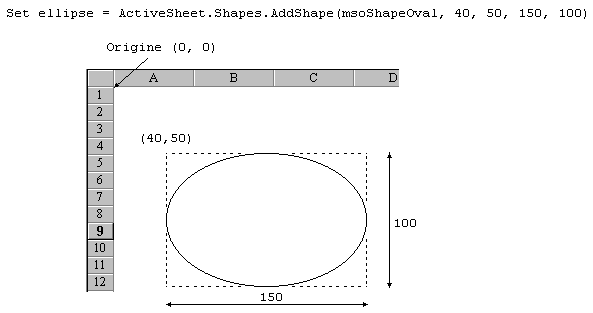
• Puis, on définit un nouveau graphique en faisant :

  ActiveSheet.ChartObjects.Add(200, 30, 350, 250).Select

  
  Les 2 premiers nombres indiquent les coordonnées du bord supérieur gauche du graphique à partir de l'origine des coordonnées écran. Cette origine se situe au coin supérieur gauche de l'écran. Les 2 derniers nombres indiquent la largeur et la hauteur du dessin. Le graphique est en même temps créé et sélectionné.

• Sur ce graphique, on applique alors la méthode ChartWizard qui permet de préciser :
  • la plage de données concernées par le graphique, dont les dimensions dépendent des paramètres Xmin, Xmax et Pas.
  • Le type du graphique (ici xlXYScatter)
  • Le sous type du graphique (ici 6)
  • Et d'autres paramètres encore.

2. Traits, rectangles et ellipses

2.1. Un exemple détaillé

Fermer le document actuel et ouvrir un nouveau document.
Dans la feuille de code associée à la feuille de calcul Feuil1, taper, puis exécuter le programme suivant :

Sub Dessin()
    ActiveWindow.DisplayGridlines = False
    ActiveSheet.DrawingObjects.Delete
    Set ligne = ActiveSheet.Shapes.AddLine(0, 0, 100, 200)
    ligne.Line.ForeColor.SchemeColor = 4
    Set Rectangle = ActiveSheet.Shapes.AddShape(msoShapeRectangle, 50, 10, 300, 150)
    Rectangle.Fill.Transparency = 0.5
    Rectangle.Fill.ForeColor.SchemeColor = 3
    Rectangle.Line.ForeColor.SchemeColor = 0
    Set ellipse = ActiveSheet.Shapes.AddShape(msoShapeOval, 40, 50, 150, 100)
    ellipse.Fill.Transparency = 1
    ellipse.Line.ForeColor.SchemeColor = 0
End Sub
  

Explications :

• La propriété DisplayGridLines permet de masquer (si false) ou d'afficher (si true) le quadrillage de la fenêtre active (en principe Feuil1).
• La méthode Delete, apliquée à l'ensemble des objets dessinés, permet d'effacer tous les objets qui auraient été préalablement dessinés sur la feuille. Cela permet de recommencer plusieurs fois l'exécution de la procédure Dessin.
• L'instructiuon Set permet de définir un objet et de lui donner un nom. Par exemple, l'objet nommé ligne est défini comme le segment dont l'origine a pour coordonnées (0,0) et l'extrémité (100,200).
• La 4ème ligne permet de préciser que l'objet ligne a la couleur n° 4 (bleu). Plus exactement, la propriété Line de l'objet Ligne a la couleur n° 4.
• La 5ème ligne ajoute un rectangle dont le coin supérieur gauche a pour coordonnées (50,10). Le paramètre 300 indique la largeur du rectangle et le dernier paramètre indique la hauteur du rectangle.
• La 6ème ligne indique que le rectangle doit être coloré de façon semi transparente (0 =opaque, 1=totalement transparent. Toutes les valeurs comprises entre 0 et 1 sont possibles)
• La 7ème ligne indique que le remplissage du rectangle se fait avec la couleur 3 (vert)
• La 8ème ligne indique que le bord du rectangle (propriété line) est de couleur 0 (noir)
• Les 3 dernières lignes définissent un objet nommé ellipse, totalement transparent, dont le pourtour est de couleur 0 (noir). Les 4 paramètres qui définissent l'ellipse sont respectivement, l'abscisse du coin supérieur gauche du rectangle circonscrit à l'ellipse, l'ordonnée de ce même point, la largeur du rectangle et la hauteur du rectangle :

• On aurait pu obtenir la même chose, de façon plus claire, en utilisant l'instruction With :

Sub Dessin()
    ActiveWindow.DisplayGridlines = False
    With ActiveSheet
        .DrawingObjects.Delete
        Set ligne = .Shapes.AddLine(0, 0, 100, 200)
        ligne.Line.ForeColor.SchemeColor = 4
        Set Rectangle = .Shapes.AddShape(msoShapeRectangle, 50, 10, 300, 150)
        With Rectangle
            .Fill.Transparency = 0.5
            .Fill.ForeColor.SchemeColor = 3
            .Line.ForeColor.SchemeColor = 0
        End With
        Set ellipse = .Shapes.AddShape(msoShapeOval, 40, 50, 150, 100)
        With ellipse
            .Fill.Transparency = 1
            .Line.ForeColor.SchemeColor = 0
        End With
    End With
End Sub

La première instruction with permet d'éviter de répéter 4 fois le mot ActiveSheet. Il est de bon usage de décaler toutes les lignes situées entre les mots with et end with de façon à bien repérer la structure. Comme on peut le voir ci-dessus, les instructions with peuvent être imbriquées les unes dans les autres.

• Pour ce qui concerne les choix des couleurs, on peut, comme ci-dessus, utiliser la palette de couleurs numérotées avec la propriété SchemeColor. On peut aussi utiliser un mélange des 3 couleurs primaires (rouge vert bleu en vidéo) grâce à la propriété RGB (red green blue). Ainsi la couleur 3 (vert) peut être obtenue en faisant :

  .Fill.ForeColor.RGB = RGB(0, 255, 0)

  Les 3 nombres nécessaires pour indiquer la couleur sont des entiers compris entre 0 et 255.

• La méthode AddShape, utilisée à 2 reprises (pour définir le rectangle puis l'ellipse), permet de définir un grand nombre de formes autres que msoShapeRectangle et msoShapeOval. Voici la liste, invraisemblable, de formes possibles :

2.2. Mettre les données dans Feuil1 et dessiner dans Feuil2

L'objectif, maintenant, est de permettre à l'utilisateur de saisir les différents éléments à dessiner (nature des objets et coordonnées ou paramètres) dans la feuille de calcul " Feuil1 " et de dessiner dans la feuille de calcul " Feuil2 ".

Il faut commencer par faire apparaître le quadrillage dans la feuille 1 : choisir la commande Outils/Options et, dans l'onglet Affichage, cocher la case Quadrillage.

Il faut maintenant effacer les 3 objets dessinés : cliquer successivement sur chacun d'eux et appuyer sur la touche 'Suppr'.

Remplir les premières cellules de la façon suivante :

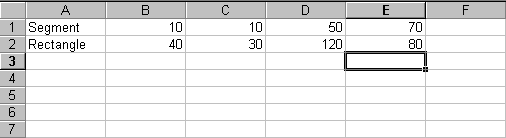
La première ligne définit un segment dont les coordonnées du point de départ sont (10 ; 10) et celles du point d'arrivée sont (50 ; 70). De même la seconde ligne définit un rectangle dont le coin supérieur gauche a pour coordonnées (40 ; 30) et le coin inférieur droit (120 ; 80).

Nous pourrons, par la suite, compléter cette page par d'autres éléments à dessiner.

Retourner dans la page de code , effacer la procédure Dessins() et taper le programme ci-dessous :

'Procédures graphiques du TP3
'ICES-Deug SV2-Mars 2002

Sub Graphiques()
    Sheets("Feuil2").Activate
    ActiveWindow.DisplayGridlines = False
    ActiveSheet.DrawingObjects.Delete
    With Sheets("Feuil1")
        For i = 1 To 10
            If .Cells(i, 1) = "Segment" Then
                Segment .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5)
            End If
        Next
    End With
End Sub

Sub Segment(x1, y1, x2, y2)
    ActiveSheet.Shapes.AddLine x1, y1, x2, y2
End Sub

Explications

• C'est la feuille 2 qui va servir de feuille de dessin, c'est donc elle que nous activons et pour laquelle nous effaçons le quadrillage et les dessins déjà présents.
• With Sheets("Feuil1") : cela permet d'alléger l'écriture qui va suivre. Nous avons déjà rencontré cette technique. Toutes les propriétés ou les méthodes qui sont utilisées entre cette ligne et la ligne End with sont relatives à l'objet Sheets("Feuil1").
• For i=1 To 10 : nous allons parcourir les 10 premières lignes de la feuille 1. L'indice i correspond donc au numéro de la ligne. Cette instruction va de pair avec l'instruction Next.
• If .Cells(i, 1) = "Segment" Then
     Segment .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5)
  End If
  Si la ligne n° i contient, dans sa première cellule, le mot " Segment ", alors...
  
• Segment ... : Appel de la procédure Segment en lui transmettant les 4 paramètres nécéssaires, contenus dans les cellules (i , 2) , (i ,3) , (i ,4) et (i ,5). Cette procédure est décrite après la fin de la procédure principale.

---

Remarque : on peut se demander pourquoi on a écrit, séparément, une procédure pour dessiner un segment alors qu'on pouvait le faire en une seule ligne. En effet, on aurait pu écrire :
If .cells(i,1) = "Segment" then
   ActiveSheets.Shapes.AddLine .cells(i,2), .cells(i,3), .cells(1,4), .Cellules(i, 5)
End if

La raison est que, d'une part, il vaut mieux séparer les tâches : le programme principal détermine les objets qu'il faut dessiner et fait appel aux procédures correspondantes ; et, d'autre part, nous allons par la suite modifier la procédure Segment pour l'améliorer.
Par ailleurs, on n'utilise pas l'écriture Set Ligne = ... car, ici, on n'a pas besoin de nommer l'objet pour lui préciser sa couleur (la couleur utilisée est le noir par défaut).

---

Il s'agit maintenant, dans les exercices qui suivent, de compléter le programme ci-dessus pour permettre de tracer des rectangles, des ellipses, des triangles, des droites, etc...

3. Exercices

3.1. Ajout d'une procédure pour dessiner des rectangles

Ajouter un second bloc If... End If qui permettra de déterminer si la cellule de la ligne i, colonne 1, contient le mot " Rectangle " et qui utilisera une procédure Rectangle. Les 4 paramètres transmis à la procédure Rectangle seront successivement l'abscisse, puis l'ordonnée du coin supérieur gauche, puis l'abscisse et enfin l'ordonnée du coin inférieur droit. Ajouter aussi, naturellement, la procédure Rectangle après la procédure Segment. Pour dessiner seulement le contour du rectangle on pourra choisir l'une des méthodes suivantes :

Sub Rectangle(x1, y1, x2, y2)
    Segment x1, y1, x2, y1
    Segment x2, y1, x2, y2
    Segment x2, y2, x1, y2
    Segment x1, y2, x1, y1
End Sub

Sub Rectangle(x1, y1, x2, y2)
    ActiveSheet.Shapes.AddShape msoShapeRectangle, x1, y1, x2 - x1, y2 - y1
End Sub

La seconde méthode est certes plus courte mais le rectangle ainsi défini masque partiellement le trait qui est dessous. Par contre, l'objet rectangle est dessiné en un seul bloc alors qu'avec la première méthode, le rectangle est formé de 4 objets séparés : les 4 segments.

Si on veut utiliser la seconde méthode, sans que le rectangle n'efface les objets qui sont dessous, il faut modifier la procédure ainsi :

Sub Rectangle(x1, y1, x2, y2)
    Set Rect = ActiveSheet.Shapes.AddShape(msoShapeRectangle, x1, y1, x2 - x1, y2 - y1)
    Rect.Fill.Transparency = 1
End Sub

3.2. Ajout d'un bouton sur la feuille 1

Ajouter un bouton que l'on pourra nommer Dessiner et qui sera relié à la procédure Graphiques

3.3. Remplacement des blocs If ... End If par une structure plus commode

Il existe une méthode plus souple et plus efficace que les multiples blocs If ... End If. La structure adaptée à ce genre de situation existe dans tous les langages de programmation. En langage VBA, elle se nomme Select case. L'intérêt de cette instruction est que l'évaluation de l'expression contenue dans la cellule (i , 1) n'est faite qu'une seule fois. Voici comment modifier cette instruction :

Sub Graphiques()
    Sheets("Feuil2").Activate
    ActiveWindow.DisplayGridlines = False
    ActiveSheet.DrawingObjects.Delete
    With Sheets("Feuil1")
        For i = 1 To 10
            Select Case .Cells(i, 1)
                Case "Segment"
                    Segment .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5)
                Case "Rectangle"
                    Rectangle .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5)
                Case "Ellipse"
                    Ellipse .Cells(i, 2), .Cells(i, 3), .Cells(i, 4), .Cells(i, 5)
            End Select
        Next i
    End With
End Sub

Ajouter également une procédure Ellipse permettant de dessiner une ellipse. On fera en sorte que les 4 paramètres transmis soient respectivement l'abscisse du centre de l'ellipse, l'ordonnée du centre, puis le demi-axe horizontal (" rayon " horizontal) et enfin, le demi-axe vertical (" rayon " vertical). En effet, d'un point de vue mathématique, une ellipse peut aussi bien être déterminée ainsi. Comme pour le rectangle, si on veut que l'intérieur de l'ellipse dessinée ne masque pas les dessins situés derrière, il faut obligatoirement préciser que la couleur de l'intérieur est transparante.

3.4. Ajout d'une procédure permettant de dessiner un triangle

La particularité du triangle (par rapport à tous les autres objets dessinés jusqu'ici) est qu'il faut préciser non pas 4 paramètres mais 6 : il y a, dans un triangle, 3 sommets, et, pour chacun d'eux, il y a 2 coordonnées.

• Dans un premier temps, on définira une procédure " Triangle " qui dessinera succesivement les 3 côtés du triangle en faisant appel 3 fois de suite à la procédure Segment.
• Dans un deuxième temps, on utilisera la méthode suivante :

Sub Triangle(x1, y1, x2, y2, x3, y3)
    Dim Sommet(1 To 4, 1 To 2) As Single
    Sommet(1, 1) = x1
    Sommet(1, 2) = y1
    Sommet(2, 1) = x2
    Sommet(2, 2) = y2
    Sommet(3, 1) = x3
    Sommet(3, 2) = y3
    Sommet(4, 1) = x1
    Sommet(4, 2) = y1
    Set Tri = ActiveSheet.Shapes.AddPolyline(Sommet)
    Tri.Fill.Transparency = 1
End Sub

Cette seconde méthode utilise le mot AddPolyline. Ce mot permet de dessiner une ligne polygonale fermée ou ouverte. Pour que la ligne dessinée soit fermée, il faut que les coordonnées du dernier sommet soient les mêmes que celles du premier sommet. Pour utiliser AddPolyline, il est obligatoire de définir un tableau contenant les coordonnées. Ce tableau, à 2 dimensions, doit être déclaré (instruction Dim) et rempli avec les données transmises à la procédure. L'expression " As Single " signifie que les données du tableau " Sommet " sont des nombres réels de type Single (réel en simple précision)

3.5. Ajout d'une procédure permettant de dessiner un cercle

Ajouter une procédure Cercle(x, y, r) permettant de dessiner un cercle connaissant respectivement les coordonnées du centre et le rayon. Cette procédure pourra faire appel à la procédure Ell définie auparavant.

3.6. Ajout de paramètres couleurs dans toutes les procédures

Jusqu'à maintenant, les objets ont tous été dessinés dans la couleur par défaut (le noir). Il serait intéressant de pouvoir préciser la couleur à l'aide d'un nombre. Les codes des couleurs ont été donnés au cours du TP2 (utiliser SchemeColor). Pour les objets Rectangle, Ellipse, Cercle et Triangle, il faut préciser 2 couleurs : la première pour le bord et la seconde pour l'intérieur.

La feuille de calcul Feuil1 doit alors être modifiée, comme par exemple :

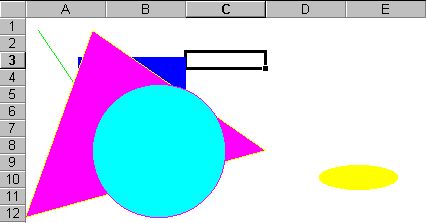
Le résultat obtenu est le suivant (avec Transparency = 0) :

3.7. Ajout d'une procédure permettant de dessiner une droite passant par 2 points A et B donnés

Cette procédure pourrait être nommée :

Sub DroiteAB(xA, yA, xB, yB, c)

où (xA , yA) sont les coordonnées du point A , (xB , yB) sont celles du point B et c désigne le code de la couleur.

Cette procédure est assez difficile à réaliser car il faut que le trait traverse tout l'écran et ne se limite pas au segment [AB].

La méthode la plus simple consiste à déterminer les coordonnées des points d'intersection de la droite avec les bords du dessin. L'abscisse minimale est toujours 0 de même que l'ordonnée minimale. Nous pouvons décider que l'abscisse maximale sera 500 (elle dépend en réalité de la configuration de l'écran) et que l'ordonnée maximale sera 400. Dans ces conditions, un algorithme pour tracer la droite AB est le suivant :

Début (procédure DroiteAB(xA,yA,xB,yB,c)
   x <— xA
   y <— yA
   dx <— xB-xA
   dy <— yB-yA
   Faire tant que (dx)2+(dy)2 > 10
      Faire tant que (x+dx>0) et (y+dy>0) et (x+dx<500) et (y+dy<400)
         x <— x+dx
         y <— y+dy
      fin tant que
      dx <— dx/2
      dy <— dy/2
   fin tant que
   x1 <— x
   y1 <— y

   dx <— xA-xB
   dy <— yA-yB
   Faire tant que (dx)2+(dy)2 > 10
      Faire tant que (x+dx>0) et (y+dy>0) et (x+dx<500) et (y+dy<400)
         x <— x+dx
         y <— y+dy
      fin tant que
      dx <— dx/2
      dy <— dy/2
   fin tant que
   x2 <— x
   y2 <— y
   Segment x1,y1,x2,y2,c
Fin (procédure DroiteAB)